Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, AD là phân giác B A C ^
=> D là điểm chính giữa B C ⏜ => OD ⊥ BC
Mà DE là tiếp tuyến => ĐPCM
b, E C D ^ = 1 2 s đ C D ⏜ = D A C ^ = B A D ^ => Đpcm
c, HC = P 3 2 => H O C ^ = 60 0 => B O C ^ = 120 0
=> l B C ⏜ = π . R . 120 0 180 0 = 2 3 πR

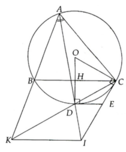
O A B D C I H M d
1) Do DB và DC là 2 tiếp tuyến của (O) => ^DBO=^DCO=900
=> Tứ giác DBOC nội tiếp đường tròn (Tâm là trung điểm OD) (1)
Xét tứ giác DHOC: ^DHO=^DCO=900
=> Tứ giác DHOC nội tiếp đường tròn (Tâm là trung điểm DO) (2)
Từ (1) và (2) => 5 điểm D,H,B,O,C cùng nằm trên 1 đường tròn (đpcm)
DB và DC là 2 tiếp tuyến của (O) => DB=DC => D thuộc trung trực của BC
Mà BC là dây cung của (O) nên O cũng thuộc trung trực của BC
=> OD \(\perp\)BC (tại I) => ^DIA=900
Xét tứ giác DIHA: ^DHA=^DIA=900 (cmt) => Tứ giác DIHA nội tiếp đường tròn (đpcm).
2) Dễ chứng minh \(\Delta\)OBI ~ \(\Delta\)ODB (g.g) => \(\frac{OB}{OD}=\frac{OI}{OB}\Rightarrow OB^2=OI.OD\)
Mà OB=OM (cùng nằm trên (O)) => \(OM^2=OI.OD\)(3)
Hoàn toàn c/m được \(\Delta\)OHD ~ \(\Delta\)OIA (g.g) => \(\frac{OH}{OI}=\frac{OD}{OA}\Rightarrow OH.OA=OI.OD\)(4)
Từ (3) và (4) => \(OM^2=OH.OA\)=> \(\frac{OM}{OA}=\frac{OH}{OM}\)
Xét \(\Delta\)OHM và \(\Delta\)OMA: \(\frac{OM}{OA}=\frac{OH}{OM}\); ^MOA chung => \(\Delta\)OHM ~ \(\Delta\)OMA (c.g.c)
=> ^OHM=^OMA. Ta có ^OHM=900 => ^OMA=900 => AM là tiếp tuyến của (O) (đpcm).
3) Ta có 5 điểm B,H,D,O,C cùng thuộc 1 đường tròn (cmt)
Suy ra Tứ giác BHOC và tứ giác DHOC nội tiếp đường tròn
Tứ giác BHOC nội tiếp đg tròn => ^ABH=^COH (Cùng bù ^HBC)
Dễ thấy ^BAH=^HDO (Cùng phụ ^DOA) (5)
Do tứ giác DHOC nôi tiếp đg tròn => ^HDO=^OCH (6)
Từ (5); (6) => ^BAH=^OCH
Xét \(\Delta\)AHB và \(\Delta\)CHO: ^ABH=^COH; ^BAH=^OCH => \(\Delta\)AHB ~ \(\Delta\)CHO (g,g)
\(\Rightarrow\)\(\frac{HB}{HO}=\frac{AH}{HC}\Rightarrow HB.HC=AH.HO\)(7)
Nhận thấy Đường tròn (O) có tiếp tuyến AM cố định (Do A cố định)
Mà MH\(\perp\)AO tại H => H cố định => AH và HO có giá trị không đổi
Nên AH.HO không đổi (8)
Từ (7) và (8) => HB.HC không đổi khi d quay quanh A (đpcm).
Xét đường tròn (O), ta có M là điểm chính giữa của cung nhỏ BC \(\Rightarrow\widebat{MB}=\widebat{MC}\)
Xét tiếp đường tròn (O) có \(\widehat{BAM}\)và \(\widehat{CAM}\)là các góc nội tiếp lần lượt chắn các cung MB và MC của (O). Mà \(\widebat{MB}=\widebat{MC}\left(cmt\right)\)\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)(trong 1 đường tròn, các góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Lại xét đường tròn (O) có CP là tiếp tuyến tại C và dây cung CM \(\Rightarrow\widehat{PCM}=\frac{1}{2}sđ\widebat{CM}\)(góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn).
Mặt khác \(\widehat{CAM}\)là góc nội tiếp chắn \(\widebat{CM}\)nên \(\widehat{CAM}=\frac{1}{2}sđ\widebat{CM}\)(trong 1 đường tròn, góc nội tiếp chắn một cung bằng nửa số đo cung bị chắn)
\(\Rightarrow\widehat{PCM}=\widehat{CAM}\left(=\frac{1}{2}sđ\widebat{CM}\right)\)
Mà \(\widehat{CAM}=\widehat{BAM}\left(cmt\right)\Rightarrow\widehat{PCM}=\widehat{BAM}\left(=\widehat{CAM}\right)\Rightarrow\widehat{PCK}=\widehat{KAP}\)
Xét tứ giác ACPK có \(\widehat{PCK}=\widehat{KAP}\left(cmt\right)\)
\(\Rightarrow\)Tứ giác ACPK nội tiếp (tứ giác có hai đỉnh kề nhìn cạnh đối diện dưới dạng các góc bằng nhau thì tứ giác đó nội tiếp)
Bạn ơi, mình vừa mới nghĩ ra cách làm này bạn xem giúp mình có đúng ko ạ,
Xét đường tròn (O) có:
∠APC và ∠AKC là 2 góc có đỉnh nằm ngoài đường tròn,
=> \(\text{∠}APC=\frac{sd\widebat{AC}-sd\widebat{MC}}{2}\)
\(\text{∠}AKC=\frac{sd\widebat{AC}-sd\widebat{MB}}{2}\)
Mà M là điểm nằm giữa cung nhỏ BC
\(=>\widebat{MC}=\widebat{MB}\)
Vậy suy ra ∠APC = ∠AKC
=> Tứ giác ACPK nội tiếp