Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Bài này có dính líu đến tứ giác nội tiếp một chút, không biết bạn học chưa. Mình sẽ cố né nội dung đó.)
\(A,O,B,C\) cùng thuộc đường tròn đường kính \(AO\).
\(B,O,C,E\) cùng thuộc đường tròn đường kính \(BE\).
(Bạn có thể chứng minh 2 điều này bằng các góc vuông)
Mà đường tròn ngoại tiếp tam giác \(BOC\) chỉ có 1 nên \(A,B,O,C,E\) cùng thuộc đường tròn.
\(AECO\) là hình thang nội tiếp nên nó là hình thang cân.
Từ đó CM được \(GA=GO,IA=IO\) và suy ra \(IG\) là đường trung trực của \(OA\).

Xét tam giác OKB có:
OI2=IK x IB
mà IB=IC (OI là đường trung trực)
=>OI2=IK x IC (1)
Xét tam giác OAB có:
BI2=OI x IA (2)
Xét tam giác vuông OBI có:
OB2=BI2+OI2=R (3)
Từ (1) và (2) và (3) =>IK x IC+OI x IA=OB2=R2 (CMX)

a) theo tính chất 2 tiếp tuyến cắt nhau => ab=ac -> a thuộc trung trực bc
từ ob = oc(gt) => o thuộc trung trực bc
từ 2 ý trên => ao là trung tực của bc => ao vuông góc bc
b) từ ao là trung trực của bc (cmt) => bh=hc
trong tam giác bdc có :
bh=hc(cmt)
ob=do(dt)
=> i là đường tb của tam giác bdc => oh song song dc=> dc song song oa
c)áp dụng định lí py ta go vào tam giác oba
ob^2 + ba^2 = oa^2
<=> 3^2 + ba^2 = 5^2
<=> ba =4 (cm)
áp dụng hệ thức lượng tam giác oba có
ba^2 = ha. oa
<=> 4^2 = ha. 5
<=> ha=302 (cm)
=> oh = 1.8 (cm)
áp dụng hệ thức lượng vào tam giác oba có
bh^2 = oh.ha
<=>bh= 2.4(cm)
mà bh=hc(cmt)=> bc=4.8(cm)
chu vi abc = ab+ bc+ac=12.8(cm)
ta có ha+ho=oa=> ha= 3.2(cm)
diện tích abc = 1/2 . ah.bc= 7.68(cm^2)
d) ta có oe vuông bd(gt)
ba vuông bd(gt)
=> oe song song ba => góc boa = góc oai (slt)(3)
trong tam giác obc có oh vuông bc (cmt) => oh là đcao
mà hb=hc(cmt)=> oh đồng thời là trung tuyến => tam giác obc cân tại o => oh là phân giác góc boc
=> góc oai = góc ioa
=> tam giác oai cân tại i
=> oi =ai
=> i thuộc trung trực oa(5)
trong tamgiác oae có góc eoa + góc oae = aeo (*)
trong tgiác oba có góc boa + góc bao = 90 độ (**)
mà aoe =bao(slt)(1)
oae = boa (slt) (2)
từ (*)(**)(1)(2) => aeo = 90 độ
xét tgiác ogc và tam giác age có aeg= ocg =90 độ
ogc=age(đối đỉnh)
=> hai tgiác đồng dạng (gg)
=> ioe=cai
ta có; ioe+eoa =ioa (7)
cai+oac =oai (8)
mà ioa = dai (cmt)(9)
ioe =cai(cmt) (10)
từ (7)(8)(9)(10) => eoa = oac
=> tgiác oag cân tại g
=> og=ag
=> g thuộc trung trực ao(6)
từ (5)(6) => ig là trung trực ao
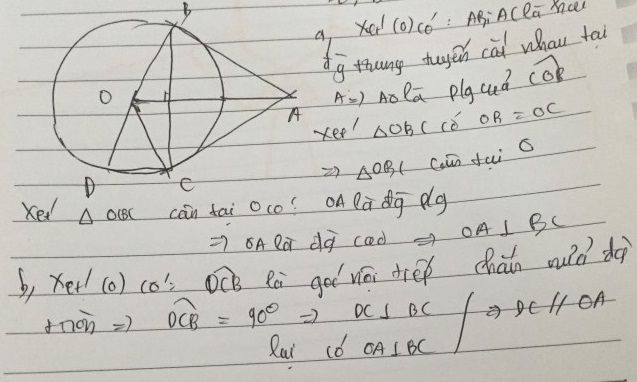
a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
OB=OC
=>O nằm trên đường trung trực của BC(1)
AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
b: Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD
mà OA\(\perp\)BC
nên OA//CD
c: Gọi H là giao điểm của BC và OA
OA là đường trung trực của BC
=>OA\(\perp\)BC tại trung điểm của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=5^2-3^2=16\)
=>BA=4(cm)
Xét ΔBOA vuông tại B có BH là đường cao
nên \(BH\cdot OA=BO\cdot BA\)
=>\(BH\cdot5=3\cdot4=12\)
=>BH=2,4(cm)
H là trung điểm của BC
=>\(BC=2\cdot BH=4,8\left(cm\right)\)
AB=AC
mà AB=4cm
nên AC=4cm
Chu vi tam giác ABC là:
AB+AC+BC
=4+4+4,8
=12,8(cm)