Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) đường thẳng y=(k-1)x+1 đi qua A(-2;3)nên thế x=-2 và y=3 vào hàm số trên ta được:
3=(k-1)(-2)+1 (với k\(\ne\)1)
-2(k-1)=2
k-1=-1
k=0
b) đường thẳng y=(k-1)x+1 không thể // với đường thẳng y=2x + 1 vì b=b' (1=1)

a) (d) đi qua điểm (1;2)
<=> 2 = k + 1 + k
<=> 1 = 2k
<=> k = 0,5
Vậy k = 0,5 thì (d) đi qua (1;2)
b) Để (d) // đgth y = 2x + 3
\(\Leftrightarrow\hept{\begin{cases}k+1=2\\k\ne3\end{cases}\Leftrightarrow\hept{\begin{cases}k=1\\k\ne3\end{cases}\Rightarrow}k=1}\)
Vậy k =1 thì (d) // đgth y = 2x +3
c) Gọi điểm cố định là (d) đi qua là (x0;y0)
Ta có y0 = ( k +1) x0 + k
<=> y0 = kx0 + x0+k
<=> y0 - x0 - k ( x0 + 1) = 0 \(\forall\)k
Để pt nghiệm đúng với mọi k <=> \(\hept{\begin{cases}x_0+1=0\\y_0-x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=-1\end{cases}}}\)
Điểm cố định (d) luôn đi qua là ( -1;-1)

a: Thay x=0 và y=0 vào (1), ta được:
k=0
c: Để (1)//\(y=\left(\sqrt{3}+1\right)x+3\), ta được:
\(\left\{{}\begin{matrix}k+1=\sqrt{3}+1\\k\ne3\end{matrix}\right.\Leftrightarrow k=\sqrt{3}\)

a: Thay x=0 và y=0 vào \(\left(d\right)\), ta được:
k=0

a, VÌ A thuộc hàm số
\(\Rightarrow3=\left(k-1\right)\left(-2\right)+1\)
\(\Leftrightarrow3=-2k+2+1\)
\(\Leftrightarrow-2k=0\)
\(\Leftrightarrow k=0\)
b. Vì 2 đường thẳng song song với nhau nên
\(\hept{\begin{cases}k-1=-3\\1\ne2\left(luondung\right)\end{cases}\Leftrightarrow k=-2}\)
Vậy ........

a, b=k=0
b,(2k-1).3+k=0 => 3k=3 => k =1
c, 2k-1 = 3/5=> 2k = 8/5 => k = 4/5 khác 4 vậy k = 4/5
d, (2k-1)(-3) +k =2 => -5k =-1 => k =1/5

Đường thẳng y = (k + 1)x + k song song với đường thẳng y = ( 3 +1)x+3 khi và chỉ khi:
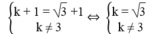
Vậy hàm số có dạng: y = ( 3 + 1)x + 3

b: Thay x=-2 và y=1/2 vào (d), ta được:
-2m+4+3m+1=1/2
=>m+5=1/2
hay m=-9/2
a, để đths y=(k-1)x+1 (k\(\ne\)1) đi qua A(-2,3) thì
3=(k-1)(-2)+1
<=> 3=-2k+2+1
<=> 0=-2k
<=>k=0( TM)
Vậy k=0 thì đths y=(k-1)x+1 đi qua A(-2;3)
b, Không có giá trị nào của k để đths y=(k-1)x+1 song song với đt y=2x+1 vì 1=1