Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Hoành độ giao điểm của (P)và (d) là:
\(\frac{1}{2}x^2=x+4\)
\(\Leftrightarrow x^2=2x+8\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left(x+2\right).\left(x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=4\end{cases}}}\)
Thay \(x=-2\)vào (d) ta được:
\(y=-2+4=2\)
Thay \(x=4\)vào (d)ta được:
\(y=4+4=8\)
Vậy \(A\left(-2;2\right),B\left(4;8\right)\)hoặc \(A\left(4;8\right),B\left(-2;2\right)\)
b)Mk ko bt làm

a) Đồ thị được vẽ như hình bên.
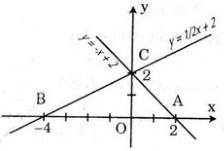
b) Giao của đường thẳng y = -x + 2 với Ox là B(2; 0).
Vì hai đường thẳng y = 0,5x + 2 và y = -x + 2 đều có tung độ gốc là 2 nên giao của chúng là C(0; 2).
Ta có tg A = 0,5. Suy ra 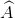 ≈ 26034’.
≈ 26034’.
Vì ∆BOC là tam giác vuông cân nên 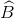 =450 .
=450 .
Suy ra 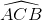 ≈ 1800 – (26034’ + 450) = 108026’.
≈ 1800 – (26034’ + 450) = 108026’.
c) Ta có AB = 6 (cm), AC = 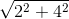 = 2√5 (cm), BC = 2√2 (cm).
= 2√5 (cm), BC = 2√2 (cm).
Do đó chu vi của ∆ABC là 6 + 2√5 + 2√2 (cm).
Diện tích của ∆ABC là:  AB . OC =
AB . OC =  . 6 . 2 = 6 (cm2).
. 6 . 2 = 6 (cm2).
Bài giải:
a) Đồ thị được vẽ như hình bên.

b) Giao của đường thẳng y = -x + 2 với Ox là B(2; 0).
Vì hai đường thẳng y = 0,5x + 2 và y = -x + 2 đều có tung độ gốc là 2 nên giao của chúng là C(0; 2).
Ta có tg A = 0,5. Suy ra 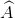 ≈ 26034’.
≈ 26034’.
Vì ∆BOC là tam giác vuông cân nên 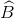 =450 .
=450 .
Suy ra 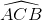 ≈ 1800 – (26034’ + 450) = 108026’.
≈ 1800 – (26034’ + 450) = 108026’.
c) Ta có AB = 6 (cm), AC = 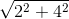 = 2√5 (cm), BC = 2√2 (cm).
= 2√5 (cm), BC = 2√2 (cm).
Do đó chu vi của ∆ABC là 6 + 2√5 + 2√2 (cm).
Diện tích của ∆ABC là:  AB . OC =
AB . OC =  . 6 . 2 = 6 (cm2).
. 6 . 2 = 6 (cm2).

1) Tìm được \(A\left(0:3\right);B\left(0:7\right)\)
\(\Rightarrow I\left(0;5\right)\)
2) Hoành độ giao điểm J của \(\left(d_1\right)\)và\(\left(d_2\right)\)là nghiệm của \(PT:x+3=3x+7\)
\(\Rightarrow x=-2\Rightarrow y_J=1\Rightarrow J\left(-2;1\right)\)
\(\Rightarrow OI^2=0^2+5^2=25\)
\(\Rightarrow OJ^2=2^2+1^2=5\)
\(\Rightarrow IJ^2=2^2+4^2=20\)
\(\Rightarrow OJ^2+IJ^2=OI^2\Rightarrow\Delta OIJ\)LÀ TAM GIÁC VUÔNG TẠI J
\(\Rightarrow S_{\Delta OIJ}=\frac{1}{2}OI.OJ=\frac{1}{2}.\sqrt{5}.\sqrt{20}=5\left(đvdt\right)\)


a) Xem hình trên
b) A(2; 4), B(4; 4).
Tính chu vi ∆OAB.
Dễ thấy AB = 4 - 2 = 2 (cm).
Áp dụng định lý Py-ta-go, ta có:
OA = 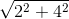 = 2√5 (cm), OB =
= 2√5 (cm), OB = 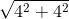 = 4√2 (cm).
= 4√2 (cm).
Tính diện tích ∆OAB.
Gọi C là điểm biểu diễn số 4 trên trục tung, ta có:
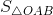 =
=  -
- 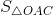 =
=  OC . OB -
OC . OB -  OC . AC.
OC . AC.
=  . 42 -
. 42 -  . 4 . 2 = 8 - 4 = 4 (cm2).
. 4 . 2 = 8 - 4 = 4 (cm2).



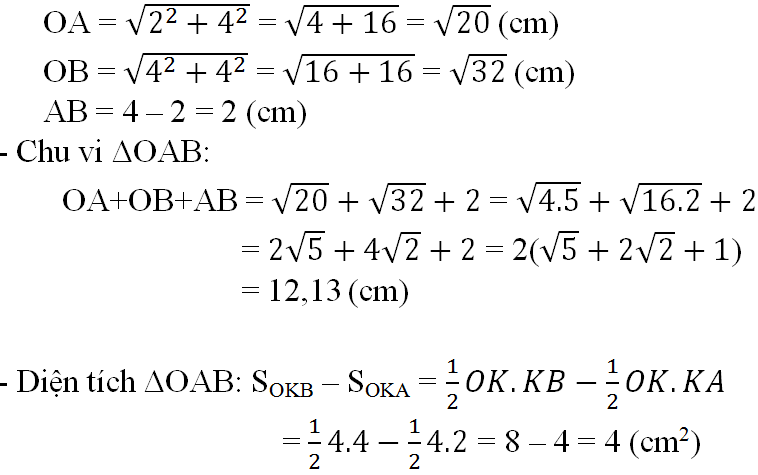
A (x; 0) là giao điểm của d với trục hoành nên 0 = − 2 x ⇔ x = − 2 ⇒ A ( − 2 ; 0 )
B (0; y) là giao điểm của d với trục tung nên y = − 2 . 0 – 4 ⇔ y = − 4 ⇒ B ( 0 ; − 4 )
Suy ra O A = | − 2 | = 2 ; O B = | − 4 | = 4
Vì tam giác )AB vuông tại O nên S O A B = O A . O B 2 = 2.4 2 = 4 (đvdt)
Đáp án cần chọn là: B