Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d
b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d

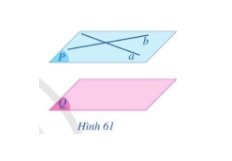
Nếu hai mặt phẳng (P) và (Q) có một điểm chung thì chúng có đường thẳng chung d.
Ta có: a // (Q);
a ⊂ (P);
(P) ∩ (Q) = d.
Suy ra a // d.
Tương tự ta cũng có b // d.
Mà a, b, d cùng nằm trong mặt phẳng (P) nên a // b // d, điều này mâu thuẫn với giả thiết a, b cắt nhau trong (P).
Vậy hai mặt phẳng (P) và (Q) không có điểm chung hay (P) // (Q).

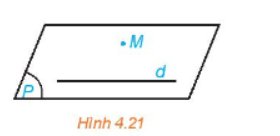
a) Có duy nhất một đường thẳng đi qua M song song với d
b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) vì hai đường thẳng song song đồng phẳng

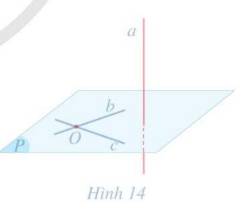
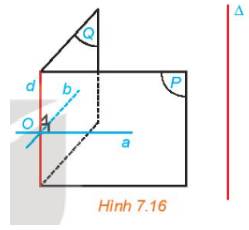
\(\left. \begin{array}{l}a \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot a\)
\(\left. \begin{array}{l}b \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot b\)
Mà \(a \cap b = \left\{ O \right\}\) \( \Rightarrow \) mp(a, b) đi qua O và vuông góc với \(\Delta \).

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

Tham khảo:
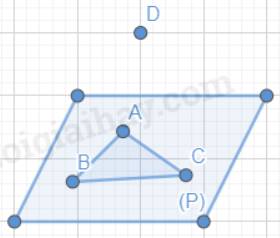
Tồn tại một và chỉ 1 mặt phẳng chứa hai đường thẳng AD và BD

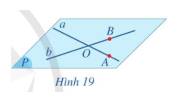
a) Mặt phẳng đi qua ba điểm A. B, O đi qua hai đường thẳng a và b
b) Có một và chỉ một mặt phẳng đi qua hai đường thẳng a và b
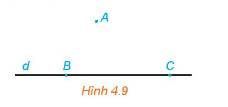
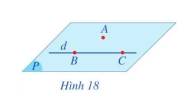

Mặt phẳng (ABC) chứa điểm A và đường thẳng d.
Do đó mp(ABC) cũng chứa hai đường thẳng AB và BC.