Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Chọn \(t = 0;t = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {1; - 2} \right),B\left( { - 1; - 1} \right)\)
b) +) Thay tọa độ điểm C vào phương trình đường thẳng \(\Delta \) ta có: \(\left\{ \begin{array}{l}1 = 1 - 2t\\ - 1 = - 2 + t\end{array} \right.\). Do hệ phương trình vô nghiệm nên C không thuộc đường thẳng \(\Delta \)
+) Thay tọa độ điểm D vào phương trình đường thẳng \(\Delta \) ta có: \(\left\{ \begin{array}{l}1 = 1 - 2t\\3 = - 2 + t\end{array} \right.\). Do hệ phương trình vô nghiệm nên D không thuộc đường thẳng \(\Delta \)
Đáp án: A
Vì d vuông góc với d’ nên d sẽ nhận vecto chỉ phương của d’ làm vecto pháp tuyến
Vậy d là đường thẳng đi qua M và có vecto pháp tuyến là 
d: -1(x - 2) - 2(y + 3) = 0 ⇔ -x - 2y - 4 ⇔ x + 2y + 4 = 0
Phương trình hoành độ giao điểm:
\(x^2+3x=x+m^2\Leftrightarrow x^2+2x-m^2=0\)
Pt đã cho luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2\end{matrix}\right.\)
Do I là trung điểm đoạn AB \(\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{x_A+m^2+x_B+m^2}{2}=m^2-1\end{matrix}\right.\)
Mà I thuộc d'
\(\Leftrightarrow y_I=2x_I+3\Leftrightarrow m^2-1=2.\left(-1\right)+3\)
\(\Leftrightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
\(\Rightarrow\sum m^2=4\)
Đáp án A
*Gọi (Q) là mặt phẳng chứa d và vuông góc với mặt phẳng (Oxy). Để khoảng cách giữa hai đường thẳng d và ∆ nhỏ nhất thì ∆ chính là giao tuyến của hai mặt phẳng (Oxy) và mp (Q).
* Mặt phẳng (Oxy) có phương trình là z = 0 có VTPT n Oxy → = (0; 0; 1).
Đường thẳng d đi qua A(1;2; -3) và có VTCP u d → = (1; -2; 0)
Suy ra, VTPT của (Q) là n Q → = [ u d → ; n Oxy → ] = (2; 1; 0)
Phương trình mặt phẳng (Q) là: 2(x - 1) + 1(y - 2) + 0(z + 3) = 0
Hay 2x + y -4 =0
* Đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (Oxy) và (Q). Tập hợp các điểm thuộc ∆ là nghiệm hệ phương trình: 
* Đặt x = 1 + t thay vào (1) ta được: y = 4 - 2x = 4 - 2(1 + t) = 2 - 2t
Suy ra, phương trình tham số của đường thẳng ∆ là: 
Ta có : \(MA=5\leftrightarrow x^2+\left(y-1\right)^2=5^2\)
Thay tọa độ điểm x,y vào tham số t vào pt trên ta được :
\(\left(2+2t\right)^2+\left(3+t-1\right)^2=25\)
\(\Leftrightarrow4t^2+8t+4+4+4t+t^2=25\)
\(\Leftrightarrow5t^2+12t-17=0\rightarrow t_1=1;t_2=-\dfrac{17}{5}\)
Với \(t_1=1\), ta được điểm \(x=4;y=4\Rightarrow M_1\left(4;4\right)\)
Với \(t_2=-\dfrac{17}{5}\)ta được điểm \(x=-\dfrac{24}{5};y=-\dfrac{2}{5}\Rightarrow M_2\left(-\dfrac{24}{5};-\dfrac{2}{5}\right)\)
Lời giải:Điểm M,N có vẻ không có vai trò gì trong bài toán.
Ta có: $\overrightarrow{u_{\Delta}}=(2,-1)$
$\overrightarrow{u_{d'}}=(a,b)$
\(\cos (\Delta, d')=\frac{\overrightarrow{u_{\Delta}}.\overrightarrow{u_d'}}{|\overrightarrow{u_{\Delta}}||\overrightarrow{u_d'}|}=\frac{2a-b}{\sqrt{a^2+b^2}.\sqrt{5}}=\cos 45^0=\frac{\sqrt{2}}{2}\)
$\Rightarrow a=3b$ hoặc $a=-\frac{b}{3}$
PTĐT $d'$ là:
$-x+3y=0$ hoặc $3x+y=0$
Tại sao từ cos 450=\(\dfrac{\sqrt{2}}{2}\) thì lại => a=3b hoặc a=\(\dfrac{-b}{3}\) ạ ?
+) Gọi A là giao điểm của đường thẳng d với trục tung
Suy ra tọa độ của A là: \(A\left( {0;y} \right)\)
Thay \(x = 0\) vào phương trình \(\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\) ta có: \(\left\{ \begin{array}{l}0 = 2 - t\\y = 5 + 3t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 2\\y = 11\end{array} \right.\)
Vậy giao điểm của d với trục tung là \(A\left( {0;11} \right)\)
+) Gọi B là giao điểm của đường thẳng d với trục hoành
Suy ra tọa độ của B là: \(B\left( {x;0} \right)\)
Thay \(y = 0\) vào phương trình \(\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\) ta có: \(\left\{ \begin{array}{l}x = 2 - t\\0 = 5 + 3t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{11}}{3}\\t = - \frac{5}{3}\end{array} \right.\)
Vậy giao điểm của d với trục hoành là \(B\left( {\frac{{11}}{3};0} \right)\)
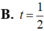
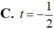
Do A nằm trên d nên thay tọa độ điểm A vào phương trình tham số đường thẳng d: