Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)

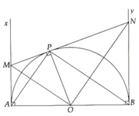
a, Sử dụng các tứ giác nội tiếp chứng minh được P M O ^ = P A O ^ và P N O ^ = P B O ^ => ∆MON và ∆APB đồng dạng (g.g)
b, Theo tính chất hai tiếp tuyến cắt nhau ta có: MP = MA và NP = NB
Mặt khác MP.NP = P O 2 và PO = R Þ AM.BN = R 2 (ĐPCM)
c, Ta có A M = R 2 => M P = R 2
Mặt khác A M = R 2 => BN = 2R => PN = 2R
Từ đó tìm được MN = 5 R 2
Vì DMON và DAPB đồng dạng nên S M O N S A P B = M N A B 2 = 25 16
d, Khi quay nửa đường tròn đường kính AB xung quanh AB ta được hình cầu với tâm O và bán kính R' = OA = R
Thể tích hình cầu đó là V = 4 3 πR 3 (đvdt)

Gọi AB giao MN là T
MN giao CD là K
Tam giác TAM đồng dạng TBN
KMD đồng dạng KNC
=>\(\frac{TA}{TB}=\frac{TM}{TN}=\frac{KM}{KN}=\frac{KD}{KC}=\frac{AD}{BC}\)
M,N cố định => K trùng T => đpcm

a: Xét (O) có
OM là bán kính
EF\(\perp\)OM tại M
Do đó: EF là tiếp tuyến của (O)
b: Xét (O) có
EM,EA là các tiếp tuyến
Do đó: EM=EA
Xét (O) có
FM,FB là các tiếp tuyến
Do đó: FM=FB
Ta có: EF=EM+MF
mà EM=EA và FM=FB
nên EF=EA+FB

a: Xét (O) có
OM là bán kính
EF vuông góc OM tại M
Do đó: EF là tiếp tuyến của (O)
b: Xét (O) có
EM.EA là tiếp tuyến
nên EM=EA
Xét(O) có
FM,FB là tiếp tuyến
nên FM=FB
EF=EM+MF
=>EF=EA+FB
