Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ABCD là hình bình hành => AB//CD mà AM thuộc AB; CN thuộc CD => AM//CN
Mà AM=CN
=> AMCN là hình bình hành (tứ giác có cặp cạnh đối // và = nhau là hình bình hành)
=> AC và MN là đường chéo của hbh AMCN
Gọi O là giao của AC và MN => O là trung điểm của AC và MN (Trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
A cố định C cố định => O cố định => MN luôn đi qua O cố định

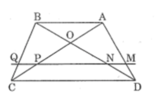
Xét Tam giác ADB: MN // AB (gt)
Suy ra: DN/DB = MN/AB (Hệ quả định lí Talét) (1)
Xét Tam giác ACB: PQ // AB (gt)
Suy ra: CQ/CB = PQ/AB (Hệ quá định lí Talét) (2)
Ta có: NQ sog sog AB (gt)
AB sog sog CD (gt)
Suy ra: NQ sog sog CD (cùng sog sog AB)
Xét Tam giác BDC: NQ sog sog CD (cmt)
Suy ra: DN/DB = CQ/CB (Định lí Talét) (3)
Từ (1), (2) và (3) suy ra: MN/AB = PQ/AB
Suy ra: MN = PQ (đpcm).

Gọi J là trung điểm cạnh BC, MN cắt AJ tại I.
Vì MADB và MAEC là các hình bình hành nên \(BD=MA=CE,BD||MA||CE\)
Suy ra BDEC là hình bình hành, suy ra N là trung điểm BE. Do đó NJ là đường trung bình \(\Delta BEC\)
Suy ra \(NJ||CE||AM,NJ=\frac{1}{2}CE=\frac{1}{2}AM\)
Theo định lí Thales \(\frac{IJ}{IA}=\frac{NJ}{MA}=\frac{1}{2}\). Vì AJ là trung tuyến của \(\Delta ABC\) nên I là trọng tâm \(\Delta ABC\)
Vậy MN đi qua I cố định.

a: DN/BD=DM/DA
CP/CA=CQ/CB
mà DM/DA=CQ/CB
nên DN/BD=CP/CA
b: Xét ΔDAB có MN//AB
nên MN/AB=DM/DA
Xet ΔCAB có PQ//AB
nên PQ/AB=CQ/CP
mà DM/DA=CQ/CP
nên MN=PQ

a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành

Trong ΔADB, ta có: MN // AB (gt)
Suy ra: ![]() hệ quả định lí ta-lét) (1)
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: 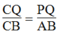 Hệ quá định lí Ta-lét) (2)
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: ![]() (Định lí Ta-lét) (3)
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra ![]() hay MN = PQ.
hay MN = PQ.