Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Kẻ CO cắt BD tại E
Xét ΔOAC vuông tại A và ΔOBE vuông tại B có
OA=OB
góc COA=góc EOB
Do đó: ΔOAC=ΔOBE
=>OC=OE
Xét ΔDCE có
DO vừa là đường cao, vừalà trung tuyến
nên ΔDEC cân tại D
=>góc DCE=góc DEC=góc CAO
=>CO là phân giác của góc DCA
Kẻ CH vuông góc với CD
Xét ΔCAO vuông tại A và ΔCHO vuông tại H có
CO chung
góc ACO=góc HCO
DO đó: ΔCAO=ΔCHO
=>OA=OH=OB và CH=CA
Xét ΔOHD vuông tại H và ΔOBD vuông tại B có
OD chung
OH=OB
Do đó: ΔOHD=ΔOBD
=>DH=DB
=>AC+BD=CD
b: AC*BD=CH*HD=OH^2=R^2=AB^2/4
=>4*AC*BD=AB^2

a: Gọi giao điểm của CO với BD là K
Xét ΔOAC vuông tại A và ΔOBK vuông tại B có
OA=OB
\(\widehat{AOC}=\widehat{BOK}\)
Do đó: ΔOAC=ΔOBK
=>OC=OK và \(\widehat{ACO}=\widehat{BKO}\)
=>\(\widehat{ACO}=\widehat{DKC}\)(1)
OC=OK
K,O,C thẳng hàng
Do đó: O là trung điểm của KC
Xét ΔDCK có
DO là đường cao
DO là đường trung tuyến
Do đó: ΔDCK cân tại D
=>\(\widehat{DCK}=\widehat{DKC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{ACO}=\widehat{HCO}\)
Xét ΔCAO vuông tại A và ΔCHO vuông tại H có
CO chung
\(\widehat{ACO}=\widehat{HCO}\)
Do đó: ΔCAO=ΔCHO
=>OA=OH=R
=>H thuộc (O)
b: Xét (O) có
OH là bán kính
CD\(\perp\)OH tại H
Do đó: CD là tiếp tuyến của (O)

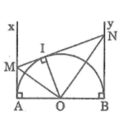
Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI
Ta có: ![]() (hai góc kề bù)
(hai góc kề bù)
OM là tia phân giác của góc AOI (tính chất hai tiếp tuyến cắt nhau)
ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)
Suy ra : OM ⊥ ON (tính chất hai góc kề bù)
Vậy ![]()

a, \(\widehat{CAI}=\widehat{CMI}=90^0\) nên ACMI nt
\(\widehat{AMB}=\widehat{EIF}=90^0\) (góc nt chắn nửa đg tròn) nên MEIF nt
b, Vì ACMI nt nên \(\widehat{MAB}=\widehat{MCI}\)
Vì MEIF nt nên \(\widehat{MEF}=\widehat{MIF}\)
Mà \(\widehat{MCI}=\widehat{MIF}\) (cùng phụ \(\widehat{MIC}\)) nên \(\widehat{MAB}=\widehat{MEF}\)
Mà 2 góc này ở vị trí ĐV nên EF//AB
c, Ta có \(\widehat{MCI}=\widehat{MIF}\)
\(\Rightarrow\widehat{MCI}+\widehat{MDI}=\widehat{MIF}+\widehat{MDI}\)
Mà tg CID vuông tại I nên \(\widehat{MCI}+\widehat{MDI}=\widehat{MIF}+\widehat{MDI}=90^0\)
Do đó tg MID vuông tại M
\(\Rightarrow\widehat{DMI}+\widehat{CMI}=90^0+90^0=180^0\)
Suy ra đpcm
Chờ t câu d
d, Gọi J,K ll là tâm đg tròn ngoại tiếp tg CME và tg MFD
Gọi G là trung điểm MF
\(\Rightarrow\widehat{GKM}=\widehat{MDF}\left(=\dfrac{1}{2}sđ\stackrel\frown{MF}\right)\)
Mà \(\widehat{GKM}+\widehat{KMG}=90^0\) nên \(\widehat{MDF}+\widehat{KMG}=90^0\left(1\right)\)
Vì MIBD nt nên \(\widehat{MBI}=\widehat{MDF}\)
Mà \(\widehat{OMB}=\widehat{OBM}\) nên \(\widehat{OMB}=\widehat{MDF}\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\widehat{OMB}+\widehat{GKM}=90^0\)
\(\Rightarrow KM\perp OM\) hay OM là tt của đg tròn ngoại tiếp tg MFD
Cmtt \(\Rightarrow JM\perp OM\) hay OM là tt đg tròn ngoại tiếp tg CME
Từ đó suy ra đpcm