Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

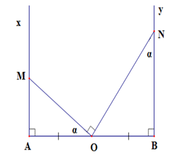
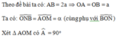
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
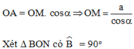
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
![]()
Vậy diện tích tam giác MON là:
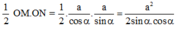
Đáp án cần chọn là: A

A B M X Y C D Drawed by Hoi con bo
Chắc mk nghĩ thế này là ổn lắm rùi
Hội con 🐄 chúc bạn học tốt!!!

bài làm
a, gọi H là tiếp điểm của tiếp tuyến MN
theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
nên ta có: MN=HM=HN=\(\dfrac{1}{2}\)(AOH =HON)=90 độ
vậy góc MON=90 đọ và là tâm giác vuông tại O đường cao OH
b,theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
Theo hệ thức lượng trong tam giác vuông: OI^2=MI.INOH2=MH.HNAM.BN=MI.NI=OI^
Vì vậy AM.BN=MI.NI=OI^2=R^2AM.BN=MH.NH=
\(OH^2\)=\(R^2\)
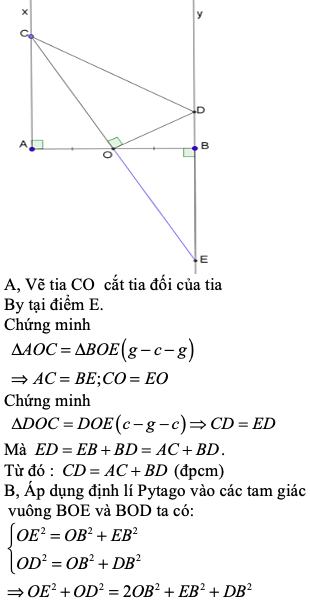
GIÚP MÌNH VỚI ,MÌNH CẦN GẤP