K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

23 tháng 10 2018
a) gọi I là trung điểm của đoạn thẳng AB
=> IA+ IB=0
| 2MI|= |BA|
|MI|= 1/2|BA|
=> M thuộc đường tròn tâm I, bán kính =1/2 BA
23 tháng 10 2018
B) gọi G là trọng tâm của tam giác ABC
=> GA+ GB+ GC=0
gọi I là trung điểm của đoạn thẳng AB
=> IA+ IB=0
| 3MG|= 3/2| 2 MI|
3| MG|= 3| MI|
| MG|= | MI|
=> M thuộc đường trung trực của đoạn thẳng GI
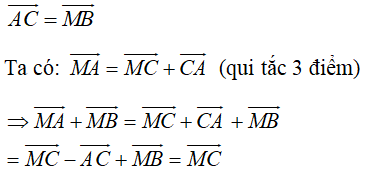
Lời giải:
Gọi $I$ là trung điểm của $AB$ thì \(\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}\)
Ta có: \(|\overrightarrow{MA}+\overrightarrow{MB}|=|\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}|=\sqrt{3}\)
\(\Leftrightarrow |2\overrightarrow{MI}|=\sqrt{3}\Leftrightarrow |\overrightarrow{MI}|=\frac{\sqrt{3}}{2}\)
Vậy tập hợp điểm M nằm trên đường tròn tâm $I$ là trung điểm của $AB$ bán kính \(\frac{\sqrt{3}}{2}\)