Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

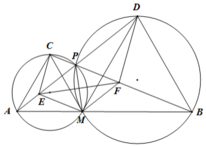
b) Vì AMPC là tứ giác nội tiếp nên
C P M = 180 o − C A M = 120 o = C M B ⇒ Δ C P M ~ Δ C M B ( g . g ) ⇒ C P C M = C M C B ⇒ C P . C B = C M 2 ⇒ C P . C B = C M .
Tương tự D P . D A = D M
Vậy C P . C B + D P . D A = C M + D M = A M + B M = A B

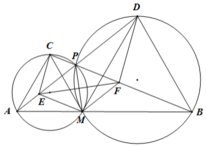
c) Ta có EF là đường trung trực của PM ⇒ EP = EM ⇒ ∆ EPM cân tại E
Mặt khác EPM = ACM = 60o (do AMPC là tứ giác nội tiếp) nên ∆ EPM đều
⇒ PE = PM . Tương tự PF = PM
Ta có CM // DB nên PCM = PBD
Mà BMPD là tứ giác nội tiếp nên PBD = PMD. Suy ra PCM = PMD
Ta lại có CPM = DPM = 120o ⇒ Δ C P M ~ Δ M P D ( g . g ) ⇒ C P M P = P M P D ⇒ C P P F = P E P D
Theo định lý Talét đảo ta có CE // DF ⇒ CDFE là hình thang.

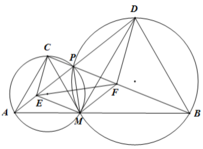
a) Vì C M A = D M B = 60 o ⇒ C M B = D M A = 120 o . Xét ∆ CMB và ∆ AMD có
C M = A M C M B = D M A ⇒ Δ C M B = Δ A M D ( c . g . c ) M B = M D ⇒ M C B = M A D M B C = M D A
Suy ra AMPC và BMPD là các tứ giác nội tiếp

Tham khảo câu a , c
https://h.vn/hoi-dap/tim-kiem?id=194717854380&q=cho%20%C4%91i%C3%AA%CC%89m%20M%20di%20%C4%91%C3%B4%CC%A3ng%20tr%C3%AAn%20%C4%91oa%CC%A3n%20th%C4%83%CC%89ng%20AB.%20Tr%C3%AAn%20cu%CC%80ng%20m%C3%B4%CC%A3t%20n%C6%B0%CC%89a%20m%C4%83%CC%A3t%20ph%C4%83%CC%89ng%20b%C6%A1%CC%80%20AB%20ve%CC%83%20ca%CC%81c%20hi%CC%80nh%20vu%C3%B4ng%20AMCD%2C%20BMEF.%C2%A0a%29%20CMR%20AE%20vu%C3%B4ng%20go%CC%81c%20BCb%29%20Go%CC%A3i%20H%20la%CC%80%20giao%20di%C3%AA%CC%89m%20cu%CC%89a%20AE%20va%CC%80%20BC.%20Ch%C6%B0%CC%81ng%20minh%20D%2CH%2CF%20th...
Không vẽ hình vì sợ duyệt nhé.
Tứ giác ADNM nội tiếp nên \(\widehat{ADM}=\widehat{ANM}\)
Tứ giác AMCD là hình vuông nên \(\widehat{ADM}=45^0\)
Từ đó \(\widehat{ANM}=45^0\)
Tứ giác BENM nội tiếp nên \(\widehat{ENM}+\widehat{EBN}=180^0\)\(\Rightarrow\widehat{ENM}=180^0-\widehat{EBM}\)
Tứ giác BMEF là hình vuông nên \(\widehat{EBM}=45^0\)
Từ đó \(\widehat{ENM}=180^0-45^0=135^0\)
Ta có \(\widehat{ANE}=\widehat{ANM}+\widehat{ENM}=45^0+135^0=180^0\)
Từ đó ta có A, N, E thẳng hàng.