Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\)
Vậy bất kì điểm M nào nằm trên mặt phẳng cũng thỏa mãn:
\(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BA}\).
b) Do \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\) nên không tồn tại điểm M thỏa mãn: \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{AB}\).
c) \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\) nên M là trung điểm của AB.
a,, CÓ \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{BA}\Leftrightarrow\overrightarrow{BA}=\overrightarrow{BA}\)
Vậy với mọi điểm M thì đều thõa mãn
b, có \(\overrightarrow{MA}-\overrightarrow{MB}=\overrightarrow{AB}\Leftrightarrow\overrightarrow{BA}=\overrightarrow{AB}\) ( không thõa mãn)
vậy không có điểm M nào thõa mãn điều kện trên
c, có \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{O}\) \(\Rightarrow\) M là trung điểm của AB

a) gọi I là trung điểm của đoạn thẳng AB
=> IA+ IB=0
| 2MI|= |BA|
|MI|= 1/2|BA|
=> M thuộc đường tròn tâm I, bán kính =1/2 BA
B) gọi G là trọng tâm của tam giác ABC
=> GA+ GB+ GC=0
gọi I là trung điểm của đoạn thẳng AB
=> IA+ IB=0
| 3MG|= 3/2| 2 MI|
3| MG|= 3| MI|
| MG|= | MI|
=> M thuộc đường trung trực của đoạn thẳng GI

a: vecto MA+2vectoMB=vecto 0
=>vecto MA=-2vecto MB
=>M nằm giữa A và B và MA=2MB
c: vecto MA+vecto MB+vecto MC=vecto 0
nên M là trọng tâm của ΔABC

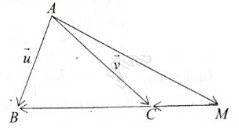
Ta có: \(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow-\overrightarrow{MB}=3\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BC}\). Mà \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\) nên \(\overrightarrow{BM}=\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
Theo quy tắc 3 điểm, ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\Rightarrow\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\) hay \(\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{u}+\dfrac{3}{2}\overrightarrow{v}\)
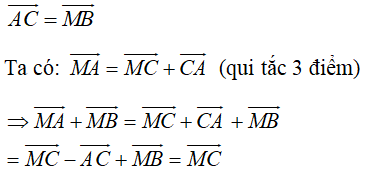
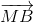 = 3
= 3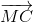 =>
=> 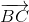 )
)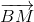 =
= 
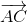 -
- 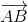 nên
nên 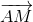 =
= 