Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

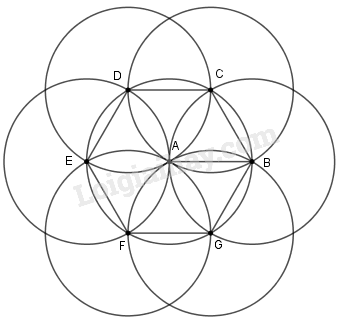
Sau khi vẽ ta được hình như sau:
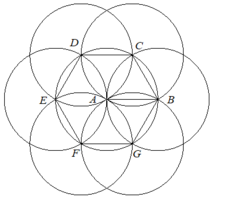
Khi đó, các đoạn thẳng A B = B C = C D = D E = E F = F G = G B (vì cùng bằng bán kính).

Sau khi vẽ ta được hình bs.17
Khi đó, các đoạn thẳng: AB, BC, CD, EF, FG, GB bằng nhau (vì cùng bằng bán kính).

a. b.
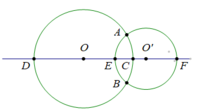
c. - Đường tròn (O’; 1cm) có đường kính là: EF; Các dây cung là: EA, EB, AB, FA, FB
Vì E thuộc (O’; 1cm) nên EO’=1cm; EF=2.EO’=2cm
- Đường tròn (O; 1,5cm) có đường kính là: DC; Các dây cung là: DA, DB, AB, AC, CB
Vì C thuộc (O; 1,5cm) nên CO=1,5cm; DC=2.CO=3cm
d. Vì đường tròn (O’; 1cm) cắt đoạn thẳng OO’ tại E, nên E nằm giữa 2 điểm O và O’.
Ta có: O E + E O ' = O O ' ⇒ O E = 1 c m
Mà EO’=1cm, nên OE=EO’ (=1cm)
Do đó: E là trung điểm của đợn thẳng OO’.
e. Vì đường tròn (O; 1cm) cắt đường thẳng OO’ tại D, đường tròn (O’; 1cm) cắt đường thẳng OO’ tại F, nên 4 điểm D, O, O’, F lần lượt theo thứ tự đó và DO=1,5cm; O’F=1cm.
Ta có: D F = D O + O O ' + O ' F = 1 , 5 + 2 + 1 = 4 , 5 c m .
Vậy DF=4,5cm

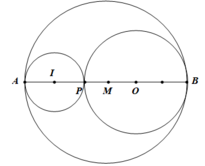
a) Điểm P, O nằm giữa A và B, AO = 4cm, BP = 4cm nên PO = 2cm, BO = 2cm.
Vậy điểm P có nằm trên đường tròn (O; 2cm).
b) Gọi M là trung điểm của AB =>AM = 3cm.
Lại có AI = 1cm => IM = 2cm
=> điểm I nằm trong đường tròn có đường kính AB ( do IM < AM ).
Có OI = 3cm > OP = 2cm nên điểm I nằm ngoài đường tròn (O; 2cm).
Vậy điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).
c) Đường tròn (I; 1cm) tiếp xúc với các đường tròn(O; 2cm) và đường tròn có đường kính AB
vì AP + PB = AB

\(a)\)Ta có:
\(M\in\left(A,3\right)\rightarrow AM=3\rightarrow BM=AB-AM=3\)
\(N\in\left(B,4\right)\rightarrow BN=4\rightarrow AN=AB-BN=2\)
\(b)\)Ta có:
\(AM=MB=\frac{1}{2}AB\left(=3\right)\)
\(\rightarrow M\)là trung điểm \(AB\)
B A M N
a)AN=6-4=2(cm)
BM=6-3=3(cm)
b)M là trung điểm của đoạn thẳng AB vì AM =BM(3cm)và M thuộc AB
Đúng thì cho mik nha, thank!
Nhận thấy tứ giác MFNE có góc M và N vuông --> góc MFN+góc MEN= 2 vuông (*)
Lại có các tam giác AFB và MEN đồng dạng (vì có góc NME=gocFAB và góc MNE =góc FBA), suy ra góc AFB=góc MEN --> góc MFN=góc MEN (**), từ (*); (**) suy ra góc MFN=góc MEN =1 vuông
--> tứ giác MENF là hình chữ nhật, từ đó dễ dàng suy ra tiếp FE vuông góc với AB
b) Gọi I ; K lần lượt là trung điểm của O1O2 và MN. Áp dụng Talét dễ dàng tính được IK=5
--> KD^2=ID^2-IK^2 =9^2 -5^2 =56 --> CD=2.KD= 4√14
Dài lắm,