Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O là trung điểm AB \(\Rightarrow OA=OB=\dfrac{AB}{2}=a\)
Áp dụng định lý Pitago:
\(AD=\sqrt{AO^2+OD^2}=\dfrac{a\sqrt{5}}{2}\)
Xét hai tam giác vuông AOD và ACB có góc A chung
\(\Rightarrow\Delta AOD\sim\Delta ACB\Rightarrow\dfrac{AD}{AB}=\dfrac{AO}{AC}\Rightarrow AC=\dfrac{AO.AB}{AD}=\dfrac{4a\sqrt{5}}{5}\)
\(BC=\sqrt{AB^2-AC^2}=\dfrac{2a\sqrt{5}}{5}\)
b. Ta có: \(AE=\sqrt{AO^2+OE^2}=a\sqrt{2}\)
\(BE=\sqrt{OB^2+OE^2}=a\sqrt{2}\)
\(\Rightarrow AE^2+BE^2=4a^2=AB^2\)
\(\Rightarrow\Delta ABE\) vuông tại E (Pitago đảo)
\(\Rightarrow\) Hai điểm E và C cùng nhìn AB dưới 1 góc vuông nên bốn điểm A,B,C,E cùng thuộc đường tròn đường kính AB (đpcm)

Lời giải:
a)
Áp dụng định lý Pitago: \(AD^2=AO^2+OD^2=a^2+(\frac{a}{2})^2=\frac{5}{4}a^2\)
\(\Rightarrow AD=\frac{\sqrt{5}a}{2}\)
\(\cos A=\frac{AO}{AD}=\frac{a}{\frac{\sqrt{5}}{2}a}=\frac{2}{\sqrt{5}}\)
Mà \(\cos A=\frac{AC}{AB}\Rightarrow AC=\cos A. AB=\frac{2}{\sqrt{5}}.2a=\frac{4}{\sqrt{5}}a\)
\(BC^2=AB^2-AC^2=(2a)^2-(\frac{4}{\sqrt{5}}a)^2=\frac{4}{5}a^2\Rightarrow BC=\frac{2}{\sqrt{5}}a\)
b)
Xét tam giác vuông tại $C$ là $CAB$ có đường trung tuyến $CO$ ứng với cạnh huyền nên \(CM=AO=OB=\frac{AB}{2}=a\)
Do đó: \(OC=OA=OB=OE=a\) nên 4 điểm $C,A,B,E$ cùng nằm trên đường tròn tâm $O$
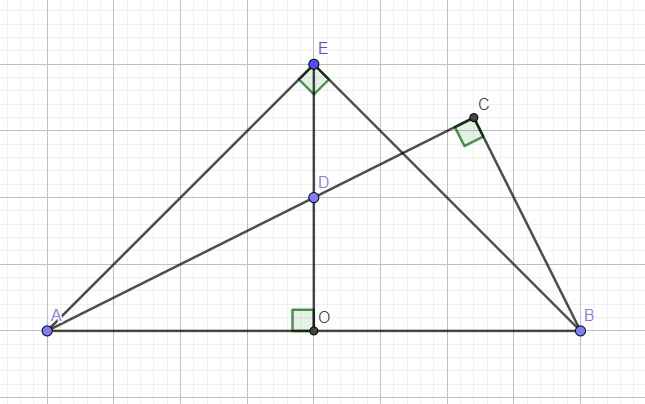

Bạn ơi cho mình hỏi, từ B kẻ BC vuông góc với AD tại đâu vậy?