Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dung kháng của tụ điện Z C = 1 C ω = 50 Ω .
→ Cảm kháng để xảy ra cực đại của điện áp hiệu dụng trên cuộn dây Z L = R 2 + Z C 2 Z C = 100 Ω → L=1/π H.
Đáp án B

Chọn B
U RL = | · Z RL = U R 2 + Z L 2 R 2 + Z L - Z C 2 ∉ R ⇔ Z L 2 = Z L - Z C 2 ⇒ Z C = 2 Z L Z = R 2 + Z L 2 = U I = 100 Ω ⇒ Z L ≤ 100 Ω ⇒ Z C = 2 Z L ≤ 200 Ω ⇒ C ≥ 1 100 π 200 = 50 π 10 - 6 F



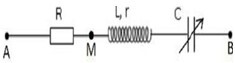
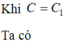
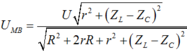

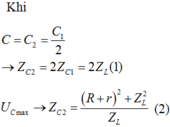

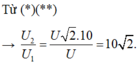


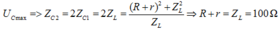
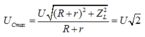
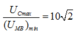
gọi điện áp hiệu dụng ở 2 đầu đoạn mạch chứa cuộn dây và tụ điện là U'.
Ta có \(U'=\frac{U\sqrt{r^2+\left(Z_L-Z_C\right)^2}}{\sqrt{\left(r+R\right)^2+\left(Z_L-Z_C\right)^2}}\) (*)
\(=\frac{U}{\sqrt{\frac{R^2+2Rr+r^2+\left(Z_L-Z_C\right)^2}{r^2+\left(Z_L-Z_C\right)^2}}}\)
\(=\frac{U}{\sqrt{1+\frac{R^2+2Rr}{r^2+\left(Z_L-Z_C\right)^2}}}\)
đặt \(y=\frac{R^2+2Rr}{r^2+\left(Z_L-Z_C\right)^2}\) với \(\left\{\begin{matrix}Z_C=x\\Z_L=m\end{matrix}\right.\) với x là biến số (do C thay đổi được), m là tham số
Dể U' đạt giá trị nhỏ nhất thì y phải đạt giá trị max.
Ta có \(y=\frac{1500}{100+m^2+x^2-2mx}\Rightarrow y'=\frac{-1500\left(2m-2x\right)}{\left(100+\left(m-x\right)^2\right)^2}\)
\(y'=0\Leftrightarrow x=m\Leftrightarrow Z_C=Z_L\)
thế lại vào (*) \(\Rightarrow U'=25V\)