Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Vì từ ω = 1 2 L C => 2ωL = 1 ω C hay 2ZL = ZC
=> ( Z L - Z C ) 2 = Z L 2
⇒ UAM = IZAM = U R 2 + ( Z L - Z C ) 2 R 2 + Z L 2 = U
UAM = U = const

\(Z_L=80\Omega\)
\(Z_C=100\Omega\)
Áp dụng điều kiện vuông pha với uRL và um :
\(\tan\varphi_{RL}.\tan\varphi_{m}=-1\)
\(\Rightarrow \dfrac{Z_L}{R}.\dfrac{Z_L-Z_C}{R}=-1\)
\(\Rightarrow \dfrac{80}{R}.\dfrac{80-100}{R}=-1\)
\(\Rightarrow R=40\Omega\)

Đáp án D
+ Dòng điện chạy qua mạch RLC có giá trị tức thời phụ thuộc vào thời gian theo quy luật hàm số sin hoặc cosin

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Giải thích: Đáp án B
+ Khi L = L1 và ω = 120π rad/s thì UL có giá trị cực đại nên sử dụng hệ quả khi UL max ta có:
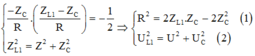
Thay U = 120 V và UC = 40 3 V ta có:
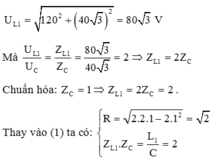
+ Khi L2 = 2L1 thì vẫn thay đổi ω để UL max nên:


Đáp án A
Tần số góc biến thiên để ULmaxnên ta có:
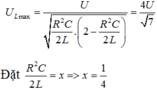
Khi tần số góc là w1thì :
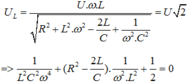
Áp dụng định lý viet phương trình có hai nghiệm phân biệt thỏa mãn:
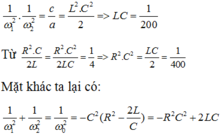
![]()
![]()


Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?

Đáp án B
+ Hai giá trị của tần số góc cho cùng dòng điện hiệu dụng trong mạch thỏa mãn
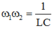
Chọn đáp án C
U L max ⇔ Z L = R 2 + Z C 2 Z C ⇔ ω L = R 2 + 1 ω 2 C 2 1 ω C ⇒ L = C R 2 + 1 ω 2 C