Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đoạn chương trình này làm công việc đổi chỗ hai phần tử m[i] và m[j] nếu m[i]>m[j]
*p/s: Đoạn chương trình này thường xuất hiện trong bài sắp xếp tăng dần của dãy số

Bài làm của bạn @lê chí hiếu(bạn được 2,1 điểm)
bài 1
program PTYN;
uses crt;
var a:array[1..100,1..100]of integer;
i,j,m,n:integer;
f1,f2:text;
Max, Min:Integer;
Kt:boolean;
Procedure XuatMang;
begin
For i:=1 to n do
begin
for j:=1 to m do
Write(a[i,j]:4);
Writeln;
end;
end;
Procedure MaxCot(l:Integer);
var p:Integer;
begin
Max:=A[1,l];
For p:=2 to n do
if A[p,l]>Max then Max:=A[p,l];
end;
Procedure MinHang(k:Integer);
var o:integer;
begin
Min:=A[k,1];
For o:=2 to n do
if A[k,o]<Min then Min:=A[k,o];
end;
begin
clrscr;
assign(f1,'ptyn.inp');
assign(f2,'ptyn.out');
reset(f1);rewrite(f2);
while not EOF(f1) do
begin
kt:=false;
readln(f1,n,m);
for i:=1 to n do
begin
for j:=1 to m do
Read(f1,a[i,j]);
readln(f1);
end;
for i:=1 to n do
begin
for j:=1 to n do
begin
MaxCot(j);
MinHang(i);
if Max=Min then
begin
Writeln(f2,'(',i,',',j,')');
kt:=true;
end;
end;
end;
If kt=false then Writeln(f2,'Khong co ptu yen ngua.');
end;
Close(f1); Close(f2);
Readln
End.
Bài 4
const fi='tvh.inp';
fo='tvh.out';
var n,d,dem,sl,s2cs,s3cs,s4cs,s5cs,s6cs,s7cs,k,i,d1:longint;
st,st1,stk:string;
f1,f2:text;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
readln(f1,n,k);
str(n,st);
d:=length(st);
case d of
1: write(9);
2: begin
sl:=n-9;
dem:=9+sl*2;
end;
3: begin
s2cs:=(99-10)+1;
s3cs:=n-99;
dem:=9+s2cs*2+s3cs*3;
end;
4: begin
s2cs:=(99-10)+1;
s3cs:=(999-100)+1;
s4cs:=n-999;
dem:=9+s2cs*2+s3cs*3+s4cs*4;
end;
5: begin
s2cs:=(99-10)+1;
s3cs:=(999-100)+1;
s4cs:=(9999-1000)+1;
s5cs:=n-9999;
dem:=9+s2cs*2+s3cs*3+s4cs*4+s5cs*5;
end;
6: begin
s2cs:=(99-10)+1;
s3cs:=(999-100)+1;
s4cs:=(9999-1000)+1;
s5cs:=(99999-10000)+1;
s6cs:=n-99999;
dem:=9+s2cs*2+s3cs*3+s4cs*4+s5cs*5+s6cs*6;
end;
7: begin
s2cs:=(99-10)+1;
s3cs:=(999-100)+1;
s4cs:=(9999-1000)+1;
s5cs:=(99999-10000)+1;
s6cs:=(999999-1000000)+1;
s7cs:=n-999999;
dem:=9+s2cs*2+s3cs*3+s4cs*4+s5cs*5+s6cs*6+s7cs*7;
end;
end;
if k<=dem then
begin
i:=1;
d1:=0;
repeat
str(i,st1);
d1:=d1+length(st1);
i:=i+1;
until d1>=k;
stk:=st1[length(st1)-(d1-k)];
writeln(f2,stk);
end;
close(f1);
close(f2);
end.
Bài 5
PROGRAM robot;
VAR A:ARRAY[0..30,0..30] OF BYTE;
F:ARRAY[0..30,0..30] OF LONGINT;
m,n:INTEGER;
PROCEDURE Enter;
VAR i,j:INTEGER;
BEGIN
readln(m,n);
FOR i:=1 TO m DO
BEGIN
FOR j:=1 TO n DO read(A[i,j]);
readln;
END;
FOR i:=0 TO m DO A[i,0]:=-1;
FOR j:=0 TO n DO A[0,j]:=-1;
END;
FUNCTION Max(a,b:LONGINT):LONGINT;
BEGINIF (a>b) THEN Max:=a ELSE Max:=b;
END;
PROCEDURE Optimize;
VAR i,j:INTEGER;
BEGIN
FOR i:=0 TO m DO F[i,0]:=-1;
FOR j:=0 TO n DO F[0,j]:=-1;
F[0,1]:=0;
FOR i:=1 TO m DO
FOR j:=1 TO n DO
F[i,j]:=2*Max(F[i,j-1],F[i-1,j])+A[i,j];
END;
PROCEDURE Trace(i,j:INTEGER);
BEGINIF (i=1) AND (j=1) THEN
writeln(F[m,n])
ELSE
BEGIN
IF F[i,j-1]>F[i-1,j] THEN
Trace(i,j-1)
ELSE
Trace(i-1,j);
writeln(i,' ',j);
END;
END;
BEGIN
Assign(Input,'Robot.inp'); Reset(Input);
Assign(Output,'Robot.out');Rewrite(Output);
Enter;
Optimize;
Trace(m,n);
close(Input);
close(Output);
END.
Em hiểu,nhưng cách anh chỉ đến 8 chữ số là cùng.
Cách em thì chỉ cần lấy int64(em dùng luôn mấy biến real vì bự hơn) thì chấp 10^30

bạn có nhập sai ct ko chứ làm sao ct chạy nếu như chưa nhập a[m] với a[j] là gì
giả sử nếu như a[m] và a[j] đã được nhập hết thì câu trả lời đúng là D

Để chứng minh tính đúng đắn của thuật toán sắp xếp chèn với các lệnh thay đổi trên, ta cần chứng minh hai điều kiện sau đây:
Điều kiện ban đầu (trước khi bắt đầu vòng lặp): Sau khi thực hiện lệnh j = 1, giá trị của j đang là 1, và dãy con A[0] chỉ gồm một phần tử là A[0] (vì j-1 là 0). Do đó, dãy con này đã được sắp xếp đúng.
Điều kiện duy trì (trong quá trình vòng lặp): Trong mỗi vòng lặp của while, nếu A[j] < A[j-1], ta hoán đổi giá trị của A[j] và A[j-1] bằng lệnh Đổi chỗ A[j] và A[j-1]. Sau đó, ta giảm giá trị của j đi 1 đơn vị bằng lệnh j = j - 1. Lúc này, giá trị của A[j] là giá trị của A[j-1] trước khi hoán đổi, và giá trị của A[j-1] là giá trị của A[j] trước khi hoán đổi. Điều này đồng nghĩa với việc dãy con A[0], A[1], ..., A[j-1] đã được sắp xếp đúng sau mỗi vòng lặp.
Vậy nên, dãy con A[0], A[1], ..., A[j-1] luôn được sắp xếp đúng sau mỗi vòng lặp của while, và dãy con này sẽ không bị thay đổi giá trị trong quá trình hoán đổi. Do đó, tính đúng đắn của thuật toán sắp xếp chèn vẫn được duy trì sau khi thay toàn bộ phần chèn A[i] vào vị trí đúng của dãy con A[0], A[1], ..., A[i-1] bằng các lệnh trên.


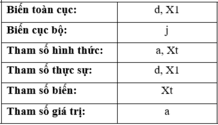


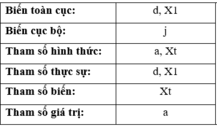
Chọn D