Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

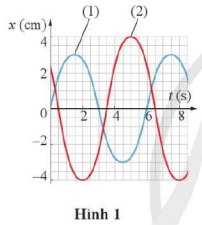
a) Dao động 1 (đường màu xanh) có:
- Biên độ: A1 = 3 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
Dao động 2 (đường màu đỏ) có:
- Biên độ: A2 = 4 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
b) Hai dao động có cùng chu kì nên \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\left(rad/s\right)\)
Độ lệch thời gian của hai dao động khi cùng trạng thái: \(\Delta t=2,5s\)
Độ lệch pha: \(\Delta\varphi=\omega.\Delta t=\dfrac{\pi}{3}\cdot2,5=150^o\)
c) Tại thời điểm 3,5 s vật 2 đang ở VTCB nên vận tốc cực đại:
\(v=\omega A_2=\text{ }\dfrac{\pi}{3}\cdot4=\dfrac{4\pi}{3}\left(cm/s\right)\)
d) Tại thời điểm 1,5 s vật 1 đang ở biên dương nên gia tốc có giá trị:
\(a=-\omega^2A_1=-\dfrac{\pi^2}{9}\cdot3=-\dfrac{\pi^2}{3}\left(cm/s^2\right)\)
Độ lớn gia tốc khi đó là \(\dfrac{\pi^2}{3}cm/s^2\)

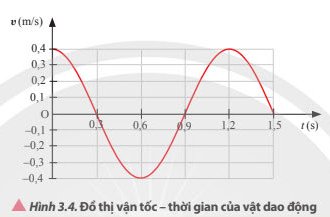
Tốc độ cực đại của vật trong quá trình dao động là 0,4 m/s
Thế năng cực đại của vật trong quá trình dao động là
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.2.0,4^2=0,16\left(J\right)\).

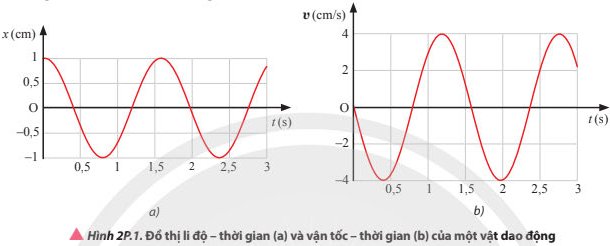
Từ đồ thị ta xác định được A = 1cm
Ta có: vmax = ωA⇒ω = 4 (rad/s)
Phương trình li độ của dao động: x = cos(4t) (cm)
Phương trình vận tốc của dao động: v = 4cos(4t+\(\frac{\pi }{2}\)) (cm/s)
Phương trình gia tốc của vật dao động: a = 16cos(4t) (m/s2)

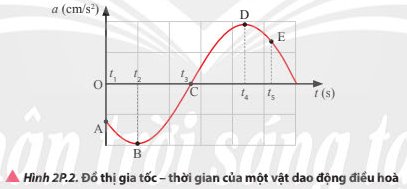
Vị trí A có gia tốc a1=−ω2.A
Vị trí B có gia tốc a2=0 nên vật ở vị trí cân bằng có vận tốc bằng v=ωA
Vị trí C có gia tốc a3=−ω2.A>0 nên vật ở vị trí biên âm có vận tốc bằng 0

a) Chu kì và tần số góc của con lắc.
Chu kì T = 1,2 s
Tần số góc là:
\(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{1,2}=5,24\left(rad/s\right)\)
b) Vận tốc cực đại của vật.
Theo đồ thì biết biên độ A = 0,35
\(v_{max}=0,35\left(m/s\right)\)
c) Cơ năng của con lắc.
\(W=\dfrac{1}{2}mv_{max}^2=\dfrac{1}{2}\cdot0,2\cdot0,35^2=0,012\left(J\right)\)
d) Biên độ của vật.
\(A=\dfrac{v_{max}}{\omega}=\dfrac{0,35}{5,24}=0,067\left(m\right)\)

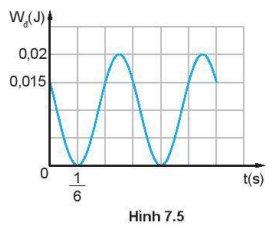
Từ đồ thị ta có:
Tại thời điểm ban đầu t = 0: Wđ = 0,015 J ⇒Wt = 0,02−0,015 = 0,005(J)
⇔\({{\rm{W}}_t} = \frac{{\rm{W}}}{4} \Rightarrow {x_0} = \pm \frac{A}{2}\)
Tại thời điểm t1 = \(\frac{1}{6}\): Wđ = 0 ⇒ x1 = ±A
Dựa vào đồ thị ta suy ra: x0 = \(\frac{A}{2}\); x1 = A
Khoảng thời gian từ x0 đến x1 là: Δt = \(\frac{T}{6}\)⇔T = 1(s) ⇔ ω = \(\frac{{2\pi }}{T} = 2\pi \) (rad/s)
\({{\rm{W}}_{{\rm{dmax}}}} = \frac{1}{2}m{\omega ^2}{A^2} = 0,02 \Leftrightarrow A = \sqrt {\frac{{{{\rm{W}}_{{\rm{dmax}}}}}}{{m{\omega ^2}}}} = \sqrt {\frac{{2.0,02}}{{0,4{{\left( {2\pi } \right)}^2}}}} = 0,05m = 5cm\)
Tại t=0:
\(\left\{ \begin{array}{c}{x_0} = A\cos \varphi = \frac{A}{2}\\v = - A\sin \varphi > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cos \varphi = \frac{1}{2}\\\sin \varphi < 0\end{array} \right. \Rightarrow \varphi = - \frac{\pi }{3}\)
Phương trình dao động của vật: x = 5cos(2πt − \(\frac{\pi }{3}\))(cm)

Vận tốc của vật vào thời điểm đó là: \(v=A\omega=\dfrac{2\pi A}{T}=\dfrac{2\pi\cdot10}{2}=10\pi\left(cm/s\right)\)
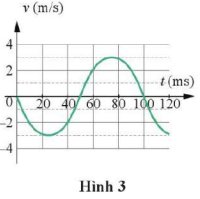


a) Chu kì T = 100 ms = 0,1 s
b) Vận tốc có độ lớn cực đại: vmax = 3 m/s
c) Tần số góc: $\omega = \frac{2 \pi}{T} =\frac{2 \pi}{0.1} = 20 \pi (rad/s)$
Biên độ của dao động: $A=\frac{v_{max}}{\omega} =\frac{3}{20 \pi} \approx 0,048m$
Cơ năng của vật dao động:
$W=W_{dmax}=\frac{1}{2}mv^{2}_{max}\frac{1}{2}.0,15.3^{2}=0,675J$
d) Tại thời điểm 100 ms vận tốc bằng 0 và đang đi theo chiều âm nên vật có vị trí tại biên dương.
Khi đó gia tốc:
$a=-\omega ^{2}A=-(20 \pi)^{2}.0,048=-19,5 m/s^{2}$