Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O x y x' y'
Vì \(\widehat{xOy}=90^0\)nên \(\widehat{x'Oy'}=\widehat{xOy}=90^0\)(đối đỉnh)
Vì \(\widehat{xOy}+\widehat{yOx'}=180^0\Rightarrow\widehat{yOx'}=180^0-90^0=90^0\)
Vì \(\widehat{yOx'}=\widehat{xOy'}\)(đối đỉnh) nên) \(\widehat{xOy'}=90^0\)
Vậy các góc xOy, x'Oy', x'Oy, xOy' đều là góc vuông.

câu này đúng này chủ tus:) i luv u chu cờ mo anh yêu em cho gờ cu

a) Góc xOy và góc .....là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
b) Góc x'Oy và góc xOy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
ghi ngắn gọn là ( ghi mỗi đáp án)
a) X'OY'
b) là hai góc đối đỉnh
+) Của cạnh OX' và cạnh OY là tia đối của cạnh OY'


x O y y' x' t t'
+) Tính \(\widehat{yOx'}\)
Ta có: \(\widehat{yOx'}+\widehat{xOy}=180^0\)(kề bù)
hay \(\widehat{yOx'}+36^0=180^0\)
\(\Leftrightarrow\widehat{yOx'}=180^0-36^0\)
\(\Leftrightarrow\widehat{yOx'}=144^0\)
Vậy \(\widehat{yOx'}=144^0\)
+) Tính \(\widehat{y'Ox'}\)
Vì hai đường thẳng xx' và yy' cắt nhau tại O nên \(\widehat{y'Ox'}\) và \(\widehat{yOx}\)là hai góc đối đỉnh.
\(\Rightarrow\widehat{y'Ox'}=\widehat{xOy}=36^0\)
Vậy \(\widehat{y'Ox'}=36^0\)
+) Tính \(\widehat{y'Ox}\)
Vì hai đường thẳng xx' và yy' cắt nhau tại O nên \(\widehat{y'Ox}\) và \(\widehat{yOx'}\)là hai góc đối đỉnh.
\(\Rightarrow\widehat{yOx'}=\widehat{xOy}'=144^0\)
Vậy \(\widehat{y'Ox}=144^0\)
b) Vì \(\widehat{y'Ox'}=\widehat{xOy}\)mà Ot là tia phân giác của \(\widehat{xOy}\),mà Ot' là tia phân giác của \(\widehat{x'Oy'}\)nên Ot và Ot' (điều hiển nhiên)




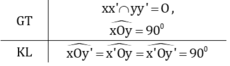
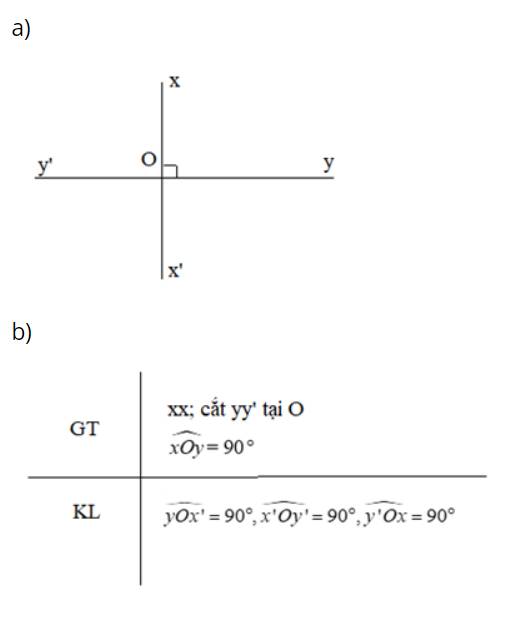
Điền vào chỗ trống: