Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+) Kẻ \(OI\perp MN;OK\perp PQ\)
\(MI^2=OM^2-OI^2\Rightarrow MN^2=4R^2-4OI^2\)
\(PK^2=OP^2-OK^2\Rightarrow PQ^2=4R^2-4OK^2\)
\(\Rightarrow MN^2+PQ^2=8R^2-4\left(OI^2+OK^2\right)=8R^2-4OH^2\)
Áp dụng đẳng thức: \(x^2+y^2=\frac{\left(x+y\right)^2}{2}+\frac{\left(x-y\right)^2}{2}\)
Ta có: \(MN^2+PQ^2=\frac{\left(MN+PQ\right)^2}{2}+\frac{\left(MN-PQ\right)^2}{2}\)
\(\Leftrightarrow\left(MN+PQ\right)^2=2\left(MN^2+PQ^2\right)-\left(MN-PQ\right)^2\)
\(\Leftrightarrow MN+PQ=\sqrt{8\left(2R^2-OH^2\right)-\left(MN-PQ\right)^2}\)
Do \(8\left(2R^2-OH^2\right)\)không đổi nên
\(\left(MN+PQ\right)_{min}\Leftrightarrow\left(MN-PQ\right)^2_{max}\Leftrightarrow\hept{\begin{cases}MN_{max}\\PQ_{min}\end{cases}}\)hoặc \(\hept{\begin{cases}MN_{min}\\PQ_{max}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}MN=2R\\PQ\perp AB\left(H\right)\end{cases}}\)hoặc \(\Leftrightarrow\hept{\begin{cases}PQ=2R\\MN\perp AB\left(H\right)\end{cases}}\)
+) \(\left(MN+PQ\right)_{max}\Leftrightarrow\left(MN-PQ\right)^2_{min}\)\(\Leftrightarrow MN=PQ\Leftrightarrow OI=OK\Rightarrow\widehat{MHA}=\widehat{PHA}=45^0\)

Gọi M, N lần lượt là trung điểm của AB, CD.
Ta có: \(P=AB+CD=2AM+2CN=2\sqrt{R^2-OM^2}+2\sqrt{R^2-ON^2}\).
Ta dễ dàng chứng minh được \(OM^2+ON^2=OI^2\).
Do đó: \(P=2\left(\sqrt{R^2-OM^2}+\sqrt{R^2-ON^2}\right)\le2\sqrt{2\left(R^2-OM^2+R^2-ON^2\right)}=2\sqrt{2\left(2R^2-OI^2\right)}\).
Đẳng thức xảy ra khi và chỉ khi \(OM=ON\), tức AB tạo với OI một góc

B O A C D K H E
a, Xét tứ giác AKCH có: \(\widehat{AKC}+\widehat{AHC}=90+90=180\)=> tứ gác AKCH nội tiếp
b,Tứ giác AKCH nội tiếp => \(\widehat{HCK}=\widehat{HAD}\)(góc trong và góc ngoài đỉnh đối diện)
Mặt khác: \(\widehat{HAD}=\widehat{BCD}=\frac{1}{2}sđ\widebat{BD}\)
=> \(\widehat{BCD}=\widehat{ACD}\)=> CD là phân giác \(\widehat{KCB}\)
c, Tứ giác AKCH nội tiếp: => \(\widehat{CKE}=\widehat{CAH}\)
Mà: \(\widehat{CDB}=\widehat{CAH}=\frac{1}{2}sđ\widebat{BC}\)
=> \(\widehat{CKE}=\widehat{CDE}\)=> tứ giác CKDE nội tiếp
=> \(\widehat{CKD}+\widehat{CED}=180\Rightarrow\widehat{CED}=180-\widehat{CKD}=180-90=90\)
=> \(CE⊥BD\)(ĐPCM)
d, em xem lại xem có gõ sai đề không nhé
Câu d) Khi C di chuyển trên cung nhỏ̉ AB. Xác định vị trí C để CK.AD+CE.DB có giá trị lớn nhất.
Nhờ mọi người giải dùm e với.

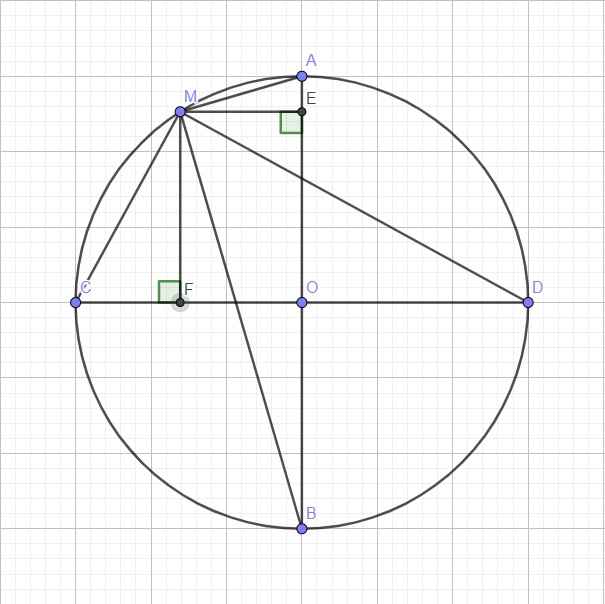
Do tính đối xứng, không mất tính tổng quát, giả sử M nằm trên cung nhỏ AC
Từ M lần lượt kẻ ME vuông góc AB và MF vuông góc CD
Do \(\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn \(\Rightarrow\widehat{AMB}=90^0\) hay tam giác AMB vuông tại M
Áp dụng hệ thức lượng: \(ME.AB=MA.MB\) \(\Leftrightarrow MA.MB=2R.ME\)
Tương tự: \(MC.MD=2R.MF\)
\(\Rightarrow MA.MB.MC.MD=4R^2.ME.MF\)
\(\Rightarrow\) Tích số đã cho đạt max khi \(ME.MF\) đạt max
Lại có tứ giác MEOF là hình chữ nhật (4 góc vuông)
\(\Rightarrow EF=MO=R\)
Áp dụng BĐT \(ab\le\dfrac{1}{2}\left(a^2+b^2\right)\) ta có:
\(ME.MF\le\dfrac{1}{2}\left(ME^2+MF^2\right)=\dfrac{1}{2}EF^2=\dfrac{1}{2}R^2\)
Dấu "=" xảy ra khi và chỉ khi \(ME=MF\) hay M nằm chính giữa cung AC
Vậy MA.MB.MC.MD đạt max khi M nằm chính giữa một trong các cung nhỏ AC, CB, BD hoặc DA

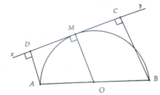
Ta có ABCD là hình thang vuông tại C và D
Mà O Là trung điểm AB và OM vuông góc với CD( tiếp tuyến của (O)
=> AD+BC=2OM=2R. Chú ý rằng CD ≤ AB (hình chiếu đường xiên)
=> S A B C D = 1 2 A D + B C . C D
= R.CD ≤ R.AB = 2 R 2
Do đó S A B C D lớn nhất khi CD=AB hay M là điểm chính giữa nửa đường tròn đường kính AB