Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

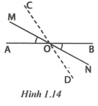
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^ mà A O M ^ = B O N ^ (hai góc đối đỉnh) nên M O C ^ = D O N ^ .
Ta có M O D ^ + D O N ^ = 180 ° (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .
Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 ° nên hai tia OC, OD đối nhau.
Chứng tỏ một tia là tia phân giác

O D C A E B
a) Ta có:
\(\widehat{DOA}=\widehat{COB}\left(=160^o-\widehat{DOC}\right)\) (1)
Mà \(\widehat{DOA}=\widehat{EOB}\) (2 góc đối đỉnh) (2)
Từ (1) và (2) \(\Rightarrow\widehat{COB}=\widehat{BOE}\left(đpcm\right)\)
b) Vì \(\widehat{COB}=\widehat{BOE}\) (cmt)
\(\Rightarrow OB\) là phân giác của \(\widehat{COE}\)
A B O C D E
a)Vì AOC=DOC nên OC là tia phân giác cảu góc AOD
b)Vì COD=BOD nên OD là tia phân giác của BOC
c)Vì OE là tia đối của tia OC nên CE là 1 tia
Vì tia OE cắt AB tại O nên A)C và BOE là 2 góc đối đỉnh(đpcm)
ban phải tính ra đã chứ