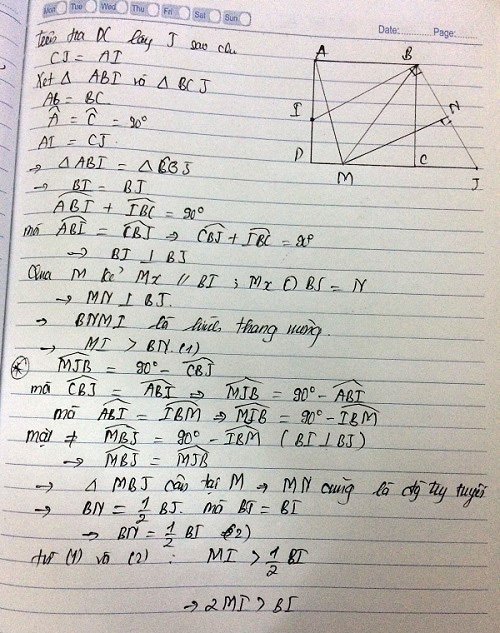Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên tia đối của tia CD em lấy điểm J sao cho CJ = AI. Qua M vẽ đường thẳng song song với BI cắt BJ tại N
Dễ cm tam giác vuông ABI = tam giác vuông CBJ => BI = BJ
Mặt khác dễ cm BI _|_ BJ => MN _|_ BJ
Và => MBJ = 900 - MBI => 900 - ABI = 900- CBJ = MJB => tam giác MBJ cân tại M => N là trung điểm của BJ
Ta có MI >= BN = BJ/2 = BI/2 ( vì BIMN là hình thang vuông tại B và N) ( đpcm)
Hay BI =< 2MI (đpcm)

mik ko hỉu lắm. để kêu là \(\le\) mà sao chỉ giải được phần < vậy.

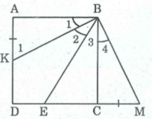
Trên tia đối của tia CD lấy điểm M sao cho CM = AK
Ta có: AK + CE = CM + CE = EM (1)
Xét ∆ ABK và ∆ CBM, ta có:
AB = CB (gt)
∠ A = ∠ C = 90 0
AK = CM (theo cách vẽ)
Suy ra: ∆ ABK = ∆ CBM (c.g.c)
⇒ ∠ B 1 = ∠ B 4 (2)
Lại có: ∠ B 1 = ∠ B 2 ( do BK là tia phân giác của ABE)
Suy ra: ∠ B 1 = ∠ B 2 = ∠ B 4
Mà ∠ (KBC) = 90 0 - ∠ B 1 (3)
Tam giác CBM vuông tại C nên: ∠ M = 90 0 - ∠ B 4 (4)
Từ (2), (3) và (4) suy ra: ∠ (KBC) = ∠ M (5)
Hay ∠ B 2 + ∠ B 3 = ∠ M
⇒ ∠ B 4 + ∠ B 3 = ∠ M( vì ∠ B 2 = ∠ B 4 )
Hay: ∠ (EBM) = ∠ M
⇒ ∆ EBM cân tại E ⇒ EM = BE. (6)
Từ (1) và (6) suy ra: AK + CE = BE.