Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(M\left(x;y\right)\) là 1 điểm bất kì thuộc d \(\Rightarrow x+3y+1=0\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép tịnh tiến nói trên thì \(M'\in d'\) với d' là ảnh của d
\(\left\{{}\begin{matrix}x'=x+3\\y'=y-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'-3\\y=y'+2\end{matrix}\right.\)
Thế vào (1):
\(x'-3+3\left(y'+2\right)+1=0\)
\(\Leftrightarrow x'+3y'+4=0\)
Vậy pt ảnh có dạng \(x+3y+4=0\)

Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow\) d' nhận (4;-3) là 1 vtpt
Phương trình d':
\(4\left(x-2\right)-3\left(y-1\right)=0\Leftrightarrow4x-3y-5=0\)
Gọi N là giao điểm của d và d' \(\Rightarrow\)tọa độ N thỏa mãn:
\(\left\{{}\begin{matrix}3x+4y+10=0\\4x-3y-5=0\end{matrix}\right.\) \(\Rightarrow N\left(-\dfrac{2}{5};-\dfrac{11}{5}\right)\)
M' là ảnh của M qua phép đối xứng trục d \(\Leftrightarrow\) N là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_N-x_M=-\dfrac{14}{5}\\y_{M'}=2y_N-y_M=-\dfrac{27}{5}\end{matrix}\right.\)
\(\Rightarrow M'\left(-\dfrac{14}{5};-\dfrac{27}{5}\right)\)
Lời giải:
Gọi $M'(a,b)$ là ảnh của $M$ đối xứng qua $d$
$\overrightarrow{MM'}=(a-2,b-1)$
Vì $\overrightarrow{MM'}\perp \overrightarrow{u_d}$ nên:
$\frac{a-2}{2}=\frac{b-1}{1}\Leftrightarrow a-2=2(b-1)(1)$
$I$ là trung điểm $MM'$. $x_I=\frac{2+a}{2}; y_I=\frac{b+1}{2}$
$3.\frac{2+a}{2}+4.\frac{b+1}{2}+10=0$
$\Leftrightarrow 3a+4b+30=0(2)$
Từ $(1);(2)\Rightarrow a=-6;b=-3$

a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2 + y 2 − 2 x + 6 y + 6 = 0 .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0.
Lấy một điểm trên d, chẳng hạn N(0; 9).
Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).
Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),
bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).
Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x − 3 2 + y − 1 2 = 4 .

Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
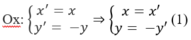
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9

Ta có: A(-1; 2) ∈ (d): 3x + y + 1 = 0.
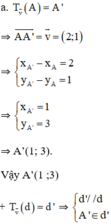
⇒ (d’): 3x + y – 6 = 0.
b. ĐOy (A) = A1 (1 ; 2)
Lấy B(0 ; -1) ∈ d
Ảnh của B qua phép đối xứng trục Oy: ĐOy (B) = B(0; -1) (vì B ∈ Oy).
⇒ d1 = ĐOy (d) chính là đường thẳng A1B.
⇒ d1: 3x – y – 1 = 0.
c. Phép đối xứng tâm O biến A thành A2(1; -2).
d2 là ảnh của d qua phép đối xứng tâm O
⇒ d2 // d và d2 đi qua A2(1 ; -2)
⇒ (d2): 3x + y – 1 = 0.
d. Gọi M(-1; 0) và N(0; 2) lần lượt là hình chiếu của A(-1; 2) trên Ox, Oy.
Q(O;90º) biến N thành N’(-2; 0), biến A thành A’, biến M thành B(0; -1).
Vậy Q(O;90º) biến hình chữ nhật ONAM thành hình chữ nhật ON’A’B. Do đó A’(-2; -1) đi qua A và B, Q(O;90º) biến A thành A’(-2; -1) biến B thành B’(1; 0)
Vậy Q(O;90º) biến d thành d’ qua hai điểm A’, B’
Do đó phương trình d’ là :
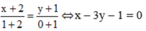
Lời giải:
Gọi $C'(a,b)$ là ảnh của $C$ đối xứng qua $x=1$
$\overrightarrow{CC'}=(a+5,b+1)\perp \overrightarrow{u_d}(1,0)$
$\Rightarrow a+5+0(b+1)=0$
$\Leftrightarrow a=-5$
$C$ đối xứng với $C'$ qua $d$ thì $CC'$ cắt $d$ tại trung điểm của nó
$\Rightarrow \frac{b-1}{2}=1$
$\Leftrightarrow b=3$
Vậy $M'(-5,3)$