Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M\in\left(d_1\right)\Rightarrow M\left(x;\dfrac{x+3}{2}\right)\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MI}\right|\) \(\left(\overrightarrow{IA}=\overrightarrow{BI}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-\dfrac{1}{2}\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{7}{2}\end{matrix}\right.\Rightarrow I\left(-\dfrac{1}{2};\dfrac{7}{2}\right)\)
\(\Rightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}\right|_{min}\Leftrightarrow\left|\overrightarrow{MI}\right|_{min}\Leftrightarrow\overrightarrow{MI}\perp\overrightarrow{AB}\Leftrightarrow\overrightarrow{MI}.\overrightarrow{AB}=0\)
\(\Leftrightarrow\left(x_I-x_M;y_I-y_M\right).\left(x_B-x_A;y_B-y_A\right)=0\)
\(\Leftrightarrow\left(x_I-x_M\right)\left(x_B-x_A\right)+\left(y_I-y_M\right)\left(y_B-y_A\right)=0\)
\(\Leftrightarrow\left(-\dfrac{1}{2}-x\right).\left(-3\right)+\dfrac{7}{2}-\dfrac{x+3}{2}=0\Rightarrow M\left(...\right)\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=2\left|\overrightarrow{MI}\right|\) nhé, đánh thiếu, nhưng nó ko ảnh hưởng gì đến bài toán :v

a) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MA} + \overrightarrow {AM} = \overrightarrow {MM} = \overrightarrow 0 \) (vì vectơ \(\overrightarrow {MB} = - \overrightarrow {MA} = \overrightarrow {AM} .\))
b) Xét hình bình hành BGCD ta có: \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GD} \)
\( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow {DG} + \overrightarrow {GD} = \overrightarrow {{\rm{DD}}} = \overrightarrow 0 \)
(vì \(\overrightarrow {GA} = - \overrightarrow {GD} = \overrightarrow {DG} \))


Vì E ; F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.
Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF.
Vậy tập hợp các điểm M thỏa mãn 2 M A → + M B → = M A → + 2 M B → là đường trung trực của đoạn thẳng AB.
Chọn A.

Chọn điểm E thuộc đoạn AB sao cho EB = 2EA ⇒ 2 E A → + E B → = 0 → .
Chọn điểm F thuộc đoạn AB sao cho FA = 2FB ⇒ 2 F B → + F A → = 0 → .
Ta có
2 M A → + M B → = M A → + 2 M B → ⇔ 2 M E → + 2 E A → + M E → + E B → = M F → + F A → + 2 M F → + 2 F B →
⇔ 3 M E → + 2 E A → + E B → ⏟ 0 → = 3 M F → + F A → + 2 F B → ⏟ 0 → ⇔ 3 M E → = 3 M F → ⇔ M E = M F . ( * )
Vì E ; F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.
Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF
Vậy tập hợp các điểm M thỏa mãn 2 M A → + M B → = M A → + 2 M B → là đường trung trực của đoạn thẳng AB.
Chọn A.

Giả sử B có tọa độ: \(B\left( {{x_B},{y_B}} \right)\)
Do M là trung điểm của đoạn thẳng AB nên: \(\left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2}\\{y_M} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2{x_M} - {x_A}\\{y_B} = 2{y_M} - {y_A}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2.5 - 2 = 8\\{y_B} = 2.7 - 4 = 10\end{array} \right.\)
Vậy tọa độ điểm B là: \(B\left( {8;10} \right)\)
Giả sử B có tọa độ: \(B\left(x_B,y_B\right)\)
Do M là trung điểm của đoạn thẳng AB nên:
\(\left\{{}\begin{matrix}x_M=\dfrac{x_A+x_B}{2}\\y_M=\dfrac{y_A+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=2x_M-x_A\\y_B=2y_M-y_A\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=2.5-2=8\\y_{B=}=2.7-4=10\end{matrix}\right.\)

Gọi giao của d và AB là C
=>C là trung điểm của AB và MC=4cm
=>CA=CB=AB/2=3cm
\(MA=MB=\sqrt{3^2+4^2}=5\left(cm\right)\)


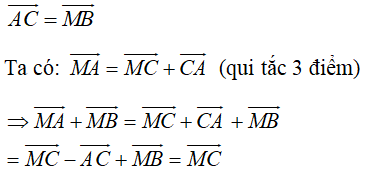
\(\overrightarrow{AB}=\left(3;-6\right)\), gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{AM}=\left(x-1;y-3\right)\)
a/ \(MA=2MB\Rightarrow\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=\frac{3}{3}\\y-3=-\frac{6}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\) \(\Rightarrow M\left(2;1\right)\)
b/ \(MB=5MA\Rightarrow\overrightarrow{AM}=\frac{1}{6}\overrightarrow{AB}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=\frac{3}{6}\\y-3=-\frac{6}{6}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\frac{3}{2}\\y=2\end{matrix}\right.\) \(\Rightarrow M\left(\frac{3}{2};2\right)\)
Ko sử dụng vecto mà làm đc ko bn