Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAH và ΔOBH có
OA=OB
\(\widehat{AOH}=\widehat{BOH}\)
OH chung
Do đó: ΔOAH=ΔOBH
Suy ra: HA=HB
b: Xét ΔOMH vuông tại M và ΔONH vuông tại N có
OH chung
\(\widehat{MOH}=\widehat{NOH}\)
Do đó: ΔOMH=ΔONH
Suy ra: HM=HN
hay ΔHMN cân tại H
c: HA=AB/2=9cm
d: Xét ΔOAB có
OM/OA=ON/OB
nên MN//AB

x y O M I H A B
xét tam giác OMI và tam giác OAI có : OI chung
IM = IA (gt)
^OIM = ^OIA = 90
=> tam giác OMI = tam giác OAI (2cgv)
=> OM = OA (1)
xét tam giác OHM và tam giác OHB có : OH chung
HB = HM (gt)
^OHB = ^OHM = 90
=> tam giác OHM = tam giác OHB (2cgv)
=> OB = OM và (1)
=> OA = OB
Hình bạn tự kẻ nha , mình ghi bải giải
Xét tam giác OAM có : OI là đường cao(Vì OI vuông góc với AM )
OI là trung tuyến(Vì I là trung điểm AM)
=> Tam giác OAM cân tại O (vì có đường cao vừa là đường trung tuyến)
=> OA = OM (1)
Xét tam giác OBM có : OH là đường cao(Vì OH vuông góc với BM)
OH là trung tuyến(Vì H là trung điểm BM)
=> Tam giác OBM cân tại O(Vì có đường cao vừa là đường trung tuyến)
=> OM = OB (2)
Từ (1) và (2) suy ra OA = OB (vì cùng bằng OM)
Học Tốt

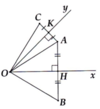
Ox là đường trung trực của AB, O AB
Nên OA = OB
Tương tự ta có OA = OC
Từ đó suy ra ĐPCM

Kẻ tia Om trong góc xOy sao cho Om // Az
Ta có hình vẽ:
x x O y A B z t m 150 150 60
Ta có: OAz + AOm = 180o (trong cùng phía)
=> 150o + AOm = 180o
=> AOm = 180o - 150o
=> AOm = 30o
Lại có: AOm + mOB = AOB = xOy
=> 30o + mOB = 60o
=> mOB = 60o - 30o
=> mOB = 30o
Do mOB + OBt = 30o + 150o = 180o mà mOB và OBt là 2 góc trong cùng phía => Om // Bt
Mặt khác, Om // Az
=> Az // Bt (đpcm)
x O y z t m A B
Giải:
Kẻ Om nằm trong góc \(\widehat{xOy}\) và OM // Az
Ta có:
\(\widehat{zAO}+\widehat{AOm}=180^o\) ( 2 góc trong cùng phía và Om // Az )
Mà \(\widehat{zAO}=150^o\Rightarrow\widehat{AOm}=30^o\)
\(\widehat{AOm}+\widehat{mOB}=60^o\)
Mà \(\widehat{AOm}=30^o\Rightarrow\widehat{mOB}=30^o\)
Ta thấy 2 góc \(\widehat{mOB}\) và \(\widehat{OBt}\) là 2 góc trong cùng phía mà \(\widehat{mOB}+\widehat{OBt}=180^o\) nên suy ra Om // Bt
Vì Om // Bt và Om // Az nên suy ra Az // Bt
\(\Rightarrowđpcm\)