Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Bn tự vẽ hình nhé )
a, Xét tam giác vuông BOH và tam giác vuông AOH có:
OH: cạnh chung
BH = AH ( giả thiết )
=> \(\Delta BOH=\Delta AOH\)( 2 cạnh góc vuông )
=> OB = OA (1)
Tương tự chứng minh \(\Delta AOK=\Delta COK\)( 2 cạnh góc vuông )
=> OA = OC (2)
Từ (1) và (2)
=> OB = OC
b, Vì \(\Delta BOH=\Delta AOH\)=> \(\widehat{BOH}=\widehat{AOH}\)
Vì \(\Delta AOK=\Delta COK\)=> \(\widehat{AOK}=\widehat{COK}\)
Ta có:
\(\widehat{BOC}=\widehat{BOH}+\widehat{AOH}+\widehat{AOK}+\widehat{COK}\)
\(\Rightarrow\widehat{BOC}=2\widehat{AOH}+2\widehat{AOK}\)
\(=2\left(\widehat{AOH}+\widehat{AOK}\right)\)
\(=2.\widehat{xOy}\)
\(=2a\)
Vậy \(\widehat{BOC}=2a\)
a. OB = OC vì đều bằng OA, bạn tự chứng minh.
b. < BOC = 2a, bạn tự chứng minh.
Nhớ tích đúng nha.

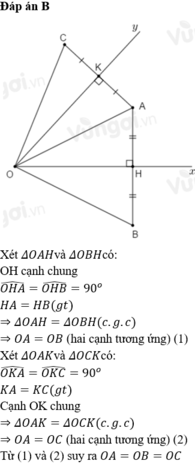
x y A O H B K C
a, Xét \(\Delta\)OKA và \(\Delta\)OKC có:
OK : cạnh chung
CK = AK (gt)
góc OKA = góc OKC = 900
=> \(\Delta\)OKA = \(\Delta\)OKC ( c - g - c)
=> OA = OC ( 2 cạnh tương ứng ) (1)
Xét \(\Delta\)OHA và \(\Delta\)OHB có:
OH : cạnh chung
AH = BH (gt)
góc OHA = góc OHB = 900
=> \(\Delta\)OHA = \(\Delta\)OHB ( c - g - c)
=> OA = OB ( 2 cạnh tương ứng ) (2)
Từ (1), (2)
=> OB = OC (dpcm)
b,
Vì \(\Delta\)OKA = \(\Delta\)OKC ( c - g - c)
=> góc COK = góc AOK = \(\dfrac{1}{2}\)góc AOC
Vì \(\Delta\)OHA = \(\Delta\)OHB ( c - g - c)
=> góc AOH = góc BOH= \(\dfrac{1}{2}\)góc AOB
Ta có:
góc AOC + góc AOB = góc BOC
=> \(\dfrac{1}{2}\)góc AOC + \(\dfrac{1}{2}\)góc AOB = \(\dfrac{1}{2}\)góc BOC
=> góc AOK + góc AOH = \(\dfrac{1}{2}\)góc BOC
=> góc xOy = \(\dfrac{1}{2}\)góc BOC
hay t = \(\dfrac{1}{2}\)góc BOC
=> góc BOC = 2t
Vậy BOC = 2t

Đáp án: \(\angle B O C = 2 \alpha\).
Lý do (ngắn gọn, dễ thấy):
Đặt \(\theta = \angle \left(\right. x , O A \left.\right)\).
Vậy
\(\angle B O C \textrm{ }\textrm{ } = \textrm{ }\textrm{ } \left(\right. 2 \alpha - \theta \left.\right) - \left(\right. - \theta \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } 2 \alpha .\)
Kết luận: \(\boxed{\angle B O C = 2 \alpha}\) (không phụ thuộc vị trí cụ thể của \(A\) trong góc nhọn \(x O y\)).
BOC=O1+O2+O3+O4
=O2+O2+O3+O3
=2O2+2O3
=2(O2+O3)
= 2 ALPHA