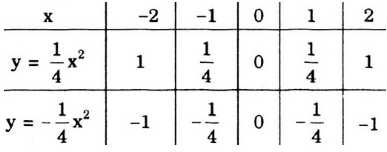
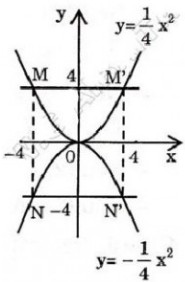
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Điểm $A$ có hoành độ $m$ thuộc đồ thị $y=x^2$ nên $A$ có tọa độ là:
\((m,m^2)\)
\(AB=\sqrt{(m-3)^2+(m^2-0)^2}=\sqrt{m^4+m^2-6m+9}\)
\(=\sqrt{m^4-2m^2+1+3m^2-6m+3+5}\)
\(=\sqrt{(m^2-1)^2+3(m-1)^2+5}\)
\(=\sqrt{(m-1)^2[(m+1)^2+3]+5}\)
\(\geq \sqrt{0+5}=\sqrt{5}\)
Ta thấy AB nhỏ nhất bằng $\sqrt{5}$ tại \((m-1)^2[(m+1)^2+3]=0\Leftrightarrow m=1\)

â ) hàm số y = ( 2m - 1 )x + m + 2 đồng biến <=> a > 0
<=> 2m - 1 > 0
<=> 2m > 1
<=> m > \(\frac{1}{2}\)
Vay : khi m > \(\frac{1}{2}\) thì hàm số trên đồng biến

a/ Với x ∈ [0;1] thì
\(f\left(x\right)=2\left(m-1\right)x+\frac{m\left(x-2\right)}{-\left(x-2\right)}=2\left(m-1\right)x-m\)
\(+m-1=0\Leftrightarrow m=1\text{ thì }f\left(x\right)=-1<0\text{ với mọi }x\in\left[0;1\right]\)
\(+m-1>0\Leftrightarrow m>1\text{ thì }2\left(m-1\right).0-m\le2\left(m-1\right)x-m\le2\left(m-1\right).1-m\)
\(\Rightarrow f\left(x\right)\le m-2\text{ với mọi }x\in\left[0;1\right]\)
Để f(x) < 0 thì m - 2 < 0 <=> m < 2.
Vậy 1 < m < 2.
\(+m-1<0\)\(\Leftrightarrow m<1\)thì \(2\left(m-1\right).1-m\le f\left(x\right)\le2\left(m-1\right).0-m\)
\(\Rightarrow f\left(x\right)\le-m\text{ với mọi }x\in\left[0;1\right]\)
Để f(x) < 0 thì -m < 0 <=> m > 0
Vậy 0 < m < 1.
Kết luận: \(m\in\left(0;2\right)\)
b/ đồ thị hàm số cắt trục hoành tại 1 điểm thuộc (1;2) <=> f(x) có 1 nghiệm trong khoảng (1;2)
Với x ∈ (1;2) thì \(f\left(x\right)=2\left(m-1\right)x-m\)
Xét phương trình \(2\left(m-1\right)x-m=0\)
\(+m=1\text{ thì pt thành }-1=0\text{ (vô lí)}\)
\(+\text{Xét }m\ne1.pt\Leftrightarrow x=\frac{m}{2\left(m-1\right)}\)
\(x\in\left(1;2\right)\Rightarrow2>\frac{m}{2\left(m-1\right)}>1\)
Giải bất phương trình trên để được \(\frac{4}{3}<\)\(m<2\)
Kết luận: \(m\in\left(\frac{4}{3};2\right)\)

khoan đã cậu ơi, tớ có hỏi gì về cạnh góc vuông đâu cậu?

Xét pt tọa độ giao điểm:
X²=(m+4)x-2m-5
<=> -x²+(m+4)x-2m-5
a=-1. b= m+4. c=2m-5
Để pt có 2 No pb =>∆>0
=> (m+4)²-4×(-1)×2m-5>0
=> m² +2×m×4+16 +8m-20>0
=> m²+9m -2>0
=> x<-9 và x>0