K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

29 tháng 5 2022
xét đường tròn \(\left(O\right)\) có \(MD\) và \(BD\) là tiếp tuyến với \(B;D\) , là tiếp điểm
\(\Rightarrow MD=DB\) ( tính chất tiếp tuyến )
xét tam giác \(MOD\) và tam giác \(BOD\) , có :
\(MD=BD\) ( cmt )
\(MO=OB\) ( cùng là bán kính đường tròn )
\(OD\) chung
\(\Rightarrow\Delta MOD=\Delta BOD\Rightarrow\) ∠ \(MDO\) \(=\) ∠ \(BDO\Rightarrow OD\) là phân giác ∠\(MDB\)
xét tam giác \(CDN\) có :
\(OD\) là đường cao ( do \(OD\perp CN\) )
\(OD\) là phân giác ∠ \(MDB\)
suy ra : tam giác \(CDN\) cân tại \(D\) , suy ra \(CD=ND\) ( đpcm )
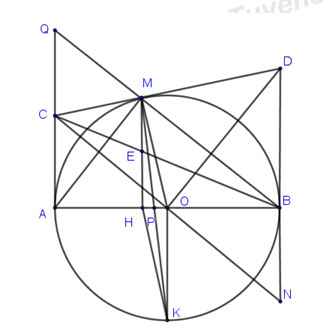
a, Ta có : AB = BQ ( tc tiếp tuyến )
OA = OQ = R
=> OB là đường trung trục
Gọi OB giao AD tại K
=> KB vuông AD ( gt ) => KB là đường cao (1)
mà OB là đường trung trục ( cmt ) => AK = KD
hay KB là đường trung tuyến (2)
Từ (1) ; (2) suy ra tam giác CBD cân => BC = BD
b, CP là tiếp tuyến ? bạn xem lại đề nhé