Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

+TXĐ: X\(\in\)R
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |

\(\left(C_1\right)\) có dạng \(y=x^3-3x\)
Gọi điểm A(a;2) là điểm kẻ đc 3 tiếp tuyến đến C do đề bài yêu cầu tìm điểm thuộc đường thẳng y=2
ta tính \(y'=3x^2-3\)
gọi \(B\left(x_0;y_0\right)\) là tọa độ tiếp điểm
phương trình tiếp tuyến tại điểm B có dạng
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
suy ra ta có \(y=\left(3x^2_0-3\right)\left(x-x_0\right)+x_0^3-3x_0\)
do tiếp tuyến đi qua điểm A suy ra tọa độ của A thỏa mãn pt tiếp tuyến ta có
\(2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0\Leftrightarrow-\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0-2=0\Leftrightarrow-3\left(x_0-1\right)\left(1+x_0\right)\left(a-x_0\right)+\left(1+x_0\right)^2\left(x_0-2\right)=0\)(*)
từ pt * suy ra đc 1 nghiệm \(x_0+1=0\Rightarrow x_0=-1\) hoặc\(-3\left(x_0-1\right)\left(a-x_0\right)+\left(1+x_0\right)\left(x_0-2\right)=0\)(**)
để qua A kẻ đc 3 tiếp tuyến thì pt (*) có 3 nghiệm phân biệt
suy ra pt (**) có 2 nghiệm phân biệt khác -1
từ đó ta suy ra đc a để pt có 2 nghiệm phân biệt khác -1
suy ra đc tập hợ điểm A để thỏa mãn đk bài ra

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

1) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/16

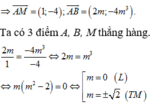
Đáp án B
Ta có y ' = 3 x 2 − 6 m x ; y ' = 0 ⇔ x 2 − 2 m x = 0 ⇔ x = 0 x = 2 m
Để hàm số đã cho có 2 điểm cực trị ⇔ m ≠ 0
Khi đó, gọi B 0 ; m , C 2 m ; m − 4 m 3 là hai điểm cực trị của ĐTHS
Lại có A B → = 1 ; m − 3 , A C → = 2 m ; m − 4 m 3
Mà A, B, C thẳng hàng ⇔ A B → = k A C → suy ra 2 m + 1 1 = m − 4 m 2 − 3 m − 3 ⇔ m = 0 ; m = 1 m = − 3 2