Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Sử dụng AQ//O'P
=> Q A P ^ = O ' A P ^ => Đpcm
b, CP//BR (cùng vuông góc AR)

a: Xét (O) có A,C,B,M cùng thuộc (O)
nên ACBM là tứ giác nội tiếp
=>\(\widehat{ACB}+\widehat{AMB}=180^0\)
mà \(\widehat{ACB}+\widehat{ECB}=180^0\)(hai góc kề bù)
nên \(\widehat{ECB}=\widehat{EMA}\)
Xét ΔECB và ΔEMA có
\(\widehat{ECB}=\widehat{EMA}\)
\(\widehat{CEB}\) chung
Do đó: ΔECB đồng dạng với ΔEMA
=>\(\dfrac{EC}{EM}=\dfrac{EB}{EA}\)
=>\(EC\cdot EA=EM\cdot EB\)
b: Ta có: OC=OD
=>O nằm trên đường trung trực của CD(1)
ta có: BC=BD
=>B nằm trên đường trung trực của CD(2)
Từ (1) và (2) suy ra OB là đường trung trực của CD
=>\(sđ\stackrel\frown{BC}=sđ\stackrel\frown{BD}\)
Xét (O) có
\(\widehat{CMB}\) là góc nội tiếp chắn cung CB
\(\widehat{DMB}\) là góc nội tiếp chắn cung BD
\(sđ\stackrel\frown{BC}=sđ\stackrel\frown{BD}\)
Do đó: \(\widehat{CMB}=\widehat{DMB}\)
=>MB là phân giác của góc DMC

a: góc ABC=1/2*sđ cung AC=90 độ
góc ABD=1/2*180=90 độ
góc CBD=góc ABC+góc ABD=90+90=180 độ
=>C,B,D thẳng hàng
b: góc AFC=1/2*sđ cung AC=90 độ
=>CF vuông góc AD
góc AED=1/2*180=90 độ
=>DE vuông góc AC
góc CED=góc CFD=90 độ
=>CEFD nội tiếp

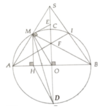
a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC