Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M . M chính là điểm cần tìm .
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’ (1). Do đó :
MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B
'A B≥
. Dấu bằng chỉ
xảy ra khi A’M’B thẳng hàng . Nghĩa là M trùng với M’
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M . M chính là điểm cần tìm .
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’ (1). Do đó :
MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B
'A B≥
. Dấu bằng chỉ
xảy ra khi A’M’B thẳng hàng . Nghĩa là M trùng với M’

M thuộc d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có : MA + MC > AC. Vậy MB + MC > AC
Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H.
Vậy khi M ≡≡ H thì : MB + MC = HB + HC = HA + HC
=> MB + MC = AC
Vậy ta có MB + MC ≥ AC
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M ≡≡ H giao điểm của AC với d

* Phân tích
Giả sử điểm M thuộc xy đã tìm được để có MA+ MB là ngắn nhất.
Lấy A’ đối xứng với A qua xy
ta có: MA = MA’
suy ra MA’ + MB cũng ngắn nhất .
Mà A và B lại nằm trên hai nửa mặt phẳng đối nhau có bờ là đường thẳng xy
Nên M phải nằm giữa A’và B tức là MA’ + MB = A’B
Suy ra M phải là giao của A’B và xy.
* Cách dựng
Dựng A’ đối xứng với A qua xy,
Nối A’với B cắt xy tại điểm M
*Chứng minh :
Nối M với A ta có MA = MA’ (A và A’ đối xứng với nhau qua xy)
Mà MA’ + MB = A’B
suy ra MA+MB =A’B là ngắn nhất
Thật vậy: nếu lấy một điểm M’ thuộc xy mà M’ khác M ,
nối M’ với A’ và M’ với B
ta có tam giác M’A’B.
Do đó M’A’ + M’B > A’B
mà M’A’ = M’A’(tính chất đối xứng).

Giả sử C là giao điểm của đoạn thẳng AB với đường thẳng d.
Vì C nằm giữa A và B nên ta có:
AC + CB = AB (1)
Lấy điểm C' bất kỳ trên d (C' ≠ C)
Nối AC', BC'
Sử dụng bất đẳng thức trong tam giác vào ∆ABC', ta có:
AC' + BC' > AB (2)
Từ (1) và (2) suy ra:
AC' + C'B > AC + CB.
Vậy điểm C cần tìm là giao điểm của đường thẳng AB với đường thẳng d.

Xét tứ giác AFBC có
N là trung điểm của AB
N là trung điểm của CF
Do đó: AFBC là hình bình hành
Suy ra: AF//BC và AF=BC
Xét tứ giác ADCB có
M là trung điểm của AC
M là trung điểm của DB
DO đó: ADCB là hình bình hành
Suy ra: AD//CB và AD=CB
Ta có: AF//BC
AD//BC
mà AD,AF có điểm chung là A
nên D,A,F thẳng hàng
mà AD=AF(=BC)
nên A là trung điểm của DF

Cậu tự vẽ hình nha !
a) Vì AB là đường trung trực của DM
=> AD = AM (tính chất 1 điểm trên đường trung trực) (1)
Tương tự với AC là trung trực của ME
=> AM = AE (2)
Từ (1) và (2)
=> AM = AD = AE
b) Từ (1) ta suy ra \(\Delta ADM\) cân tại A
Từ (2) ta cũng có \(\Delta AEM\) cân tại A
Vì trong tam giác cân , đường trung trực , phân giác , trung tuyến , đường cao đều trung nhau
=> Với AB,AC là đường trung trực tương ứng thì AB,AC cũng là phân giác tương ứng
=> \(\widehat{DAB}=\widehat{MAB}=\frac{\widehat{MAD}}{2}\) và \(\widehat{MAC}=\widehat{CAE}=\frac{\widehat{MAE}}{2}\)
Ta có :
\(\widehat{BAM}+\widehat{MAC}=90^0\)
\(2\widehat{BAM}+2\widehat{MAC}=180^0\)
\(\widehat{MAD}+\widehat{MAE}=180^0\)
=> Ba điểm thẳng hàng
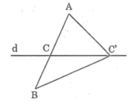
để CA + CB là nhỏ nhất
<=> CA=CB và CA vuông góc với d; CB vuông góc với d