Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{2019^2}>\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+...+\dfrac{1}{2019\cdot2020}=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{2019}-\dfrac{1}{2020}=\dfrac{1}{5}-\dfrac{1}{2020}=\dfrac{404-1}{2020}=\dfrac{403}{2020}>\dfrac{40}{2020}=\dfrac{20}{101}\left(1\right)\) \(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{2019^2}< \dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+...+\dfrac{1}{2018\cdot2019}=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{2018}-\dfrac{1}{2019}=\dfrac{1}{4}-\dfrac{1}{2019}=\dfrac{2019-4}{4\cdot2019}=\dfrac{2015}{4\cdot2019}< \dfrac{2019}{4\cdot2019}=\dfrac{1}{4}\left(2\right)\) Từ (1) và (2) \(\Rightarrow\dfrac{20}{101}< A< \dfrac{1}{4}\)

Lời giải:
$A< \frac{1}{2^2}+\frac{1}{2.3}+\frac{1}{3.4}+..+\frac{1}{99.100}$
$A< \frac{1}{4}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{100-99}{99.100}$
$A< \frac{1}{4}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}$
$A< \frac{1}{4}+\frac{1}{2}-\frac{1}{100}< \frac{1}{4}+\frac{1}{2}$
Hay $A< \frac{3}{4}$

a) Gọi ƯCLN(12n+1,30n+2) là d
12n+1⋮d ⇒ 60n+5⋮d
30n+2⋮d ⇒ 60n+4⋮d
(60n+5)-(60n+4)⋮d
1⋮d
Vậy \(\dfrac{12n+1}{30n+2}\) là ps tối giản
b) Đặt A=\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}\)
Ta có: \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{100^2}< \dfrac{1}{99.100}\)
\(A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\)
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A< 1-\dfrac{1}{100}\)
\(A< 1-\dfrac{1}{100}< 1\left(đpcm\right)\)

Câu a :
Chưa nghĩ ra! Sorry nhé!!
Câu b :
Câu hỏi của Trần Thùy Linh - Toán lớp 6 | Học trực tuyến
Câu c :
Câu hỏi của Trần Thùy Linh - Toán lớp 6 | Học trực tuyến
Vào link đó mà xem, t ngại chép lại

Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{10^2}< \dfrac{1}{9.10}\)
cộng vế với vê sta đc
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}=1-\dfrac{1}{10}=\dfrac{9}{10}< 1\)
Vậy ta có đpcm

1/2^2<1/1*2
1/3^2<1/2*3
...
1/10^2<1/9*10
=>\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}=1-\dfrac{1}{10}=\dfrac{9}{10}\)
=>A<9/10
=>A<1

Ta có:
1/2^2 > 1/2.3
1/3^2 > 1/3.4
...
1/10^2 > 1/10.11
-> Cộng dọc theo vế ta có:
1/2^2+1/3^2+...+1/10^2 > 1/2.3+1/3.4+...+1/10.11
= 1/2-1/3+1/3-1/4+...+1/10-1/11
= 1/2 - 1/11 = 9/22 (đpcm)
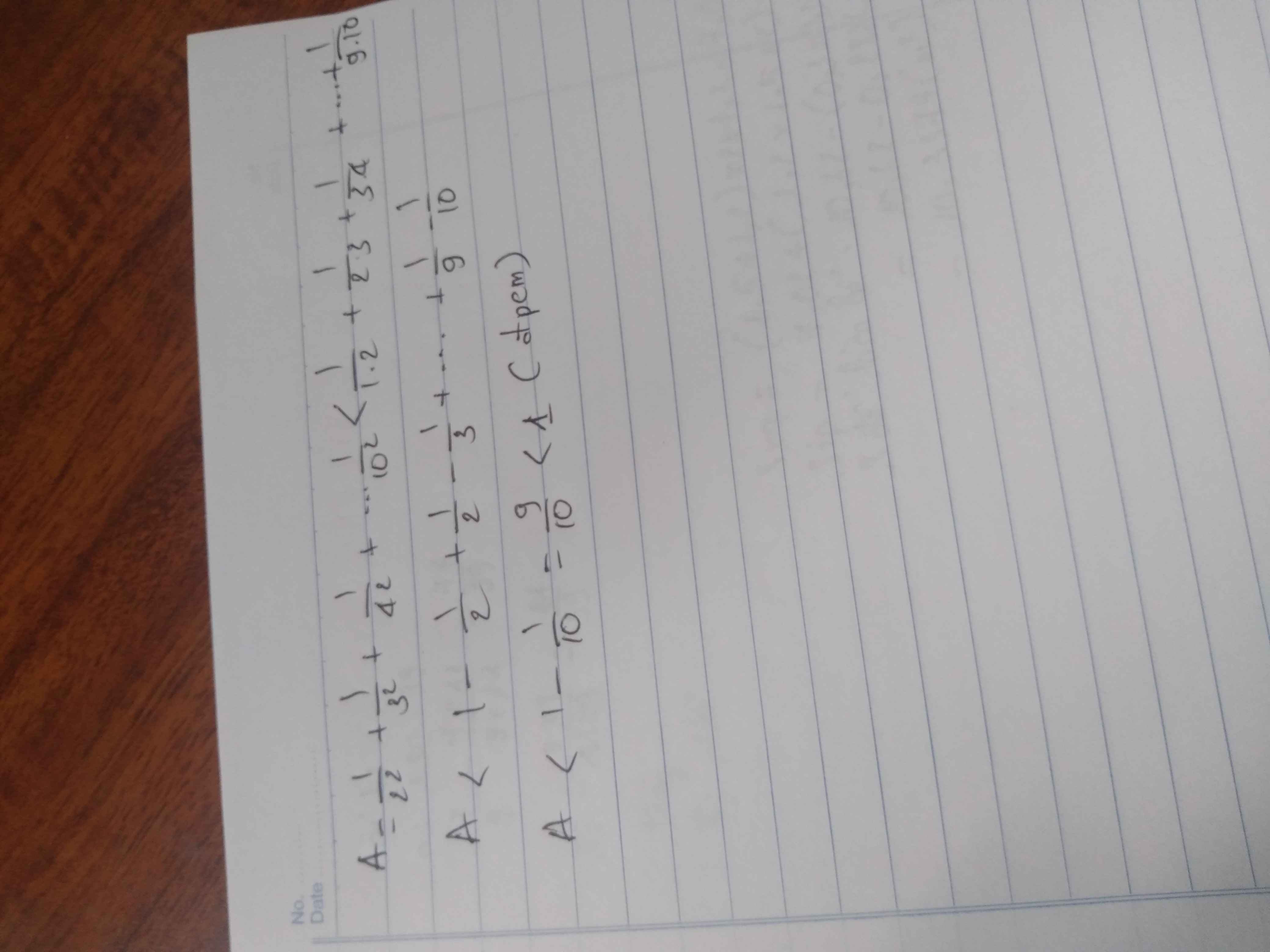
\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{20^2}\) . CMR : A<1
Giải:
Có \(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}\\ \dfrac{1}{3^2}< \dfrac{1}{2\cdot3}\\ ....\\ \dfrac{1}{20^2}< \dfrac{1}{19\cdot20}\)
Nên `A=1/2^2+1/3^2+1/4^2+...+1/(20^2)<1/1.2+1/2.3+1/3.4+...+1/19.20`
`=1-1/2+1/2-1/3+1/3-1/4+...+1/19-1/20=1-1/20=19/20`
Mà `19/20<1`
nên `A<1(đpcm)`