Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác đều ABC độ dài cạnh là 6cm. Kẻ AI vuông góc với BC. Độ dài cạnh AI là:
A. 3√3 cm
B. 3 cm
C. 3√2 cm
D. 6√3 cm

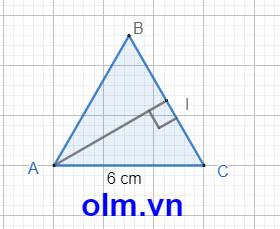
IC = \(\dfrac{1}{2}\)BC (vì trong tam giác đều đường cao cũng là trung tuyến, đường trung trực, đường phân giác của tam giác đó).
IC = 6 \(\times\) \(\dfrac{1}{2}\) = 3 (cm)
Xét \(\Delta\)AIC vuông tại C nên theo pytago ta có:
AI2 = AC2 - IC2 = 62 - 32 = 27 (cm)
AI = \(\sqrt{27}\) = 3\(\sqrt{3}\)(cm)
Chọn A. 3\(\sqrt{3}\)cm

Hình bạn tự vẽ nhá :v
Vì tam giác ABC là tam giác đều
=> AI vừa là đường cao , vừa là đường trung tuyến ứng với BC
=> I là trung điểm BC
=> IC = 6:2 = 3 cm
Xét tam giác AIC vuông tại I
Áp dụng định lí Pitago , ta có :
AI2 = IC2 + AC2
=> AI2 = 32 + 62 = 9+36 = 45
=> AI = √45 ( vì độ dài AI luôn dương)

tam giác AEC VUÔNG TẠI E,THEO ĐỊNH LÝ PYTAGO TA CÓ
AC^2=AE^2+EC^2=>AE^2=AC^2-BC^2=>AE^2=34^2-30^2=>AE=16=>EB=18
TAM GIÁC EBC VUÔNG TẠI E THEO ĐL PYAGO TA CÓ
EC^2+EB^2=BC^2=>18^2+30^2=BC^2=>BC^2=576=>BC=24
=>CẠNH ĐÁY BC =24(CM)

Ta có : Thay x,y tỉ lệ vào 4 và 3 thì : x/4 = y/3
Theo định lí Py-ta-go thì : x2 + y2 = 52 (*)
Đặt : x/4 = y/3 = t => x=4.t và y=3.t
Cũng theo định lí Py-ta-go
Thay x,y vào (*) ta có:
(4.t)2 + (3.t)2 . t2 = 52
=> { 4 + 3 }2 . t2 = 52
Do 4^2+3^2 > 5^2
Nên : t^2 = 1 => t = 1
=> x = 4.1=4 y = 3.1=3
3a 5 4a
Gọi cạnh góc vuông lần lượt là: 4a , 3a (a\(\in\) N)
Ta có :
( 3a )2 + ( 4a )2 = 52
=> 25a2 = 25
=> a2 = 1
=> a = 1
\(\Leftrightarrow\)2 cạnh góc vuông có độ dài lần lượt là : 3 ;4