Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Qua B kẻ BH // AC , cắt DM tại H
Ta có {BH // AK ; AB = BD => BH là đường trung bình của tam giác ADK
=> AK=2BH (1)
Dễ dàng chứng minh được tam giác MKC = tam giác MBH (g.c.g)
=> BH = CK (2)
Từ (1) và (2) suy ra AK = 2CK
Qua B Kẻ BH // AC , cắt DM tại H
Ta có : BH // AK
AB // BD
=> BH là đường trung bình của tam giác ADK
=> AK = 2 BH (1)
· * Xét tam giác MKC và tam giác MBH .
CÓ : BM = CM ( M là trung điểm của BC)
Góc M1= Góc M2 ( 2 góc đối đỉnh)
Góc MKC = MBH ( = 90 *)* là độ
=> Tam giác MKC = Tam giác MBH ( g. c . g)
=> BH = KC ( 2 cạnh tương ứng )(2)
Từ (1), (2) suy ra được AK = 2 KC

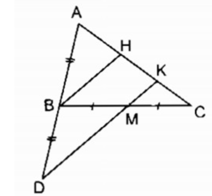
Gọi H là trung điểm của AK
Trong ∆ ADK ta có BH là đường trung bình của ∆ ADK.
⇒ BH // DK (tính chất đường trung bình của tam giác)
Hay BH // MK
Trong ∆ BCH ta có M là trung điểm của BC
MK // BH
⇒ CK = HK
AK = AH + HK = 2HK
Suy ra: AK = 2 KC ( vì HK =KC)
Lời giải:
Từ $B$ kẻ \(BT\parallel AC\)
Xét tam giác $DAK$ có \(BT\parallel AK\Rightarrow \) áp dụng định lý Thales:
\(\frac{BT}{AK}=\frac{BD}{DA}=\frac{1}{2}\Rightarrow AK=2BT(1)\) (do \(B\) là trung điểm của $AD$ )
Xét tam giác $BTM$ và $CKM$ có:
\(\left\{\begin{matrix} \angle TBM=\angle KCM(\text{so le trong})\\ \angle BMT=\angle CMK(\text{góc đối})\\ BM=MC\end{matrix}\right.\)
\(\Rightarrow \triangle BTM=\triangle CKM(g.c.g)\Rightarrow BT=CK(2)\)
Từ \((1),(2)\Rightarrow AK=2KC\) (đpcm).