Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét 2 tam giác vuông: tam giác ABH và tam giác ACK có:
AB = AC (gt)
góc A chung
suy ra: tam giác ABH = tam giác ACK (ch-gn)
b) áp dụng định lí tổng 3 góc của tam giác vào tam giác vuông ABH ta có:
góc BAH + góc ABH = 90^0
=> góc ABH = 90^0 - góc BAH
=> góc ABH = 90^0 - 50^0 = 40^0
Tam giác ABC cân tại A => \(\widehat{ABC}=\frac{180^0-\widehat{A}}{2}=65^0\)
=> góc HBC = 25^0
Tương tự: góc KCB = 25^0
suy ra: góc BOC = 130^0

a: Xét ΔABC có \(AC^2=AB^2+BC^2\)
nên ΔABC vuông tại B

Ta có: BC = HB+HC = 9+16=25cm
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=\sqrt{225}=15cm\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=\sqrt{144}=12cm\)
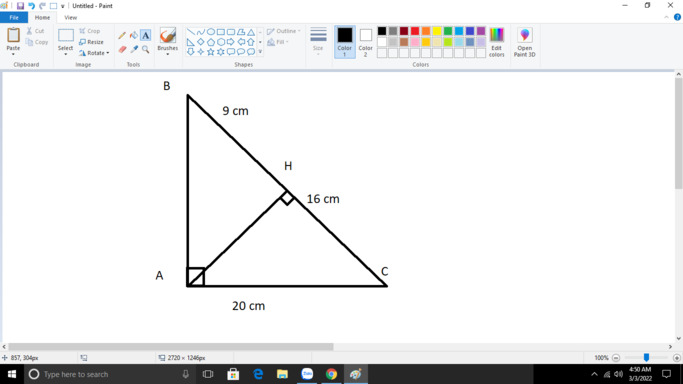
\(BC=BH+HC\)
\(\Rightarrow BC=9cm+16cm=25\left(cm\right)\)
\(\text{Xét }\Delta ABC\text{ vuông tại }A\text{ có:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow AB^2=25^2-20^2=625-400=225\left(cm\right)\)
\(\Rightarrow AB=\sqrt{225}=15\left(cm\right)\)
\(\text{Xét }\Delta AHC\text{ vuông tại }H\text{ có:}\)
\(AC^2=AH^2+HC^2\)
\(\Rightarrow AH^2-AC^2-HC^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow AH^2=20^2-16^2=400-256=144\left(cm\right)\)
\(\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)

Áp dụng định lý pytago vào\(\Delta AHB\) ta có :
AB\(^2\) = AH\(^2\) + BH\(^2\) => (\(\sqrt{18}\))\(^2\) = AH\(^2\) + 3\(^2\)
=> 18 = AH\(^2\) + 9 => AH\(^2\) = 18 - 9
=> AH\(^2\) = 9 => AH = 3 cm (do AH > 0 cm)
Mà BH = 3 cm => AH =BH
Trong \(\Delta ABH\) có AH = BH nên \(\Delta ABH\) là tam giác cân tại H
Do đó \(\widehat{A}\) = \(\widehat{ABH}\)
Áp dụng định lý tổng 3 góc của tam giác vào tam giác ABH vuông tại H có:
\(\widehat{A}\) + \(\widehat{ABH}\) = 90\(^0\) mà \(\widehat{A}\) = \(\widehat{ABH}\)
=> 2.\(\widehat{A}\) = 90\(^0\) => \(\widehat{A}\) = 45\(^0\)
Vậy \(\widehat{BAC}\) = 45\(^0\)

sửa lại :
Cho tam giác ABC cân tại A, \(\widehat{A}=30^o\). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).
Gọi I là giao điểm của BH và CK.
Tính số đo góc \(\widehat{BAI}\)
giải:
ta có : \(\Delta ABC\)cân tại A
=> AB=AC(t/c \(\Delta\)cân)
xét \(\Delta BAH\)và\(\Delta CAK\)
\(\widehat{A}-chung\)
AB=AC
\(\widehat{AKC}=\widehat{AHB}=90^o\)
=>\(\Delta BAH\)=\(\Delta CAK\)(ch-gn)
=>\(\widehat{ABH}=\widehat{ACK}\left(2ctu\right)\)
=>\(\widehat{ABI}=\widehat{ACI}\)
xét \(\Delta ABI\)VÀ \(\Delta ACI\)
AB=AC(cmt)
\(\widehat{ABI}=\widehat{ACI}\)(cmt)
AI-cạnh chung
=>\(\Delta ABI\)=\(\Delta ACI\)(cgc)
=>\(\widehat{BAI}=\widehat{CAI}\left(2gtu\right)\)
ta có : \(\widehat{BAI}+\widehat{CAI}=\widehat{A}=30^o\)
mà\(\widehat{BAI}=\widehat{CAI}\left(cmt\right)\)
=> \(\widehat{BAI}=\widehat{CAI}=15^o\)

Bài này như dùng tỉ số lượng giác lớp 9?
Mình ko biết,cô mình giao cho mình cũng k hiểu