Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tg ABH và ACK có :
AB=AC(tg ABC cân tại A)
\(\widehat{A}-chung\)
\(\widehat{AHB}=\widehat{AKC}=90^o\)
=> Tg ABH=ACK(cạnh huyền-góc nhọn) (đccm)
b) Do tg ABH=ACK (cmt)
\(\Rightarrow\widehat{ABH}=\widehat{ACK}\)
Mà : \(\widehat{ABC}=\widehat{ACB}\)(tg ABC cân tại A)
\(\Rightarrow\widehat{OBC}=\widehat{OCB}\)
=> Tg OBC cân tại O
=> OB=OC (đccm)
c) Do : AB=AC (tg ABC cân tại A)
MB=NC(gt)
=> AB+BM=AC+CN
=> AM=AN
=> Tg AMN cân tại A
\(\Rightarrow\widehat{M}=\widehat{N}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
- Do tg ABH=ACK (cmt)
=> AK=AH
=> Tg AKH cân tại A
\(\Rightarrow\widehat{AKH}=\widehat{AHK}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
- Từ (1) và (2) \(\Rightarrow\widehat{M}=\widehat{AKH}\)
Mà chúng là 2 góc đồng vị
=> KH//MN (đccm)
#H

Xét \(\Delta MKP\) vuông tại M
\(KP^2=KM^2+PM^2=\left(\frac{5}{2}\right)^2+4^2=22.25\Rightarrow KP=\sqrt{\frac{69}{2}}cm\) (1 )
Xét \(\Delta MNP\) vuông tại M
\(NP^2=MN^2+MP^2=5^2+4^2=\sqrt{41}\) (2)
Từ (1) và (2') => PN > KP
Tớ nghĩ là phải thêm bước \(PK=\sqrt{\frac{69}{2}}=\sqrt{35}cm\)
\(NP=\sqrt{41}cm\)
Ta có: \(\sqrt{41}>\sqrt{35,5}\) nên NP > PK
Cảm ơn cậu nhá ![]()

Kí hiệu tam giác viết là t/g nhé
a) BI là phân giác ABC nên ABI = CBI
Xét t/g BID vuông tại D và t/g BIF vuông tại F có:
BI là cạnh chung
DBI = FBI (cmt)
Do đó, t/g BID = t/g BIF ( cạnh góc vuông và góc nhọn kề) (đpcm)
b) t/g BID = t/g BIF (câu a) => ID = IF (2 cạnh tương ứng) (1)
C/m tương tự câu a ta cũng có: t/g ADI = t/g AEI ( cạnh góc vuông và góc nhọn kề)
=> ID = IE (2 cạnh tương ứng)
Từ (1) và (2) => ID = IE = IF (đpcm)
ban tu ve hinh nhe![]()
![]()
a) Xet tam giac BID va tam giac BIF co:
BI:canh chung
goc DBI=goc IBF(vi tia BI la tia phan giac cua goc DBF)
goc BDI=goc BFI(=90do)
Vay tam giac BID=tam giac BIF(canh huyen, goc nhon)
b) Vi tam giac BID=tam giac BIF(cau a)
Nen ID=IF(2 canh tuong ung) (1)
Xet tam giac AID va tam giac AIE co:
AI:canh chung
goc DAI=goc EAI(vi tia AI la tia phan giac cua goc DAE)
goc ADI=goc AEI(=90do)
Nen tam giac AID=tam giac AIE(canh huyen,goc nhon)
Suy ra:ID=IE(2 canh ung) (2)
Tu (1), (2)\(\Rightarrow\) IF=ID=IE
Chuc ban ngay cang hoc gioi len nhe![]()
![]()
Hen gap lai ban vao dip khac nhe![]()

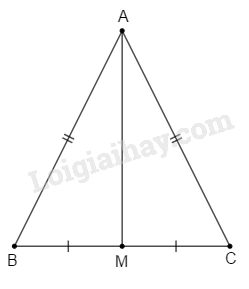
Xét \(\Delta ABC\) có:
c) Ta có \(\Delta ABC\) cân tại \(A\left(cmt\right).\)
=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân).
Xét 2 \(\Delta\) vuông \(HBM\) và \(KCM\) có:
\(\widehat{MHB}=\widehat{MKC}=90^0\left(gt\right)\)
\(BM=CM\) (như ở trên)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> \(\Delta HBM=\Delta KCM\) (cạnh huyền - góc nhọn).
=> \(HM=KM\) (2 cạnh tương ứng).
Chúc bạn học tốt!

a b c m d 1 2 3 4 e f
Xét T/G ABC và DCM
CÓ ; M1=M2 ( đối đỉnh) CM=BM (M là trung điểm BC) AM=MD (gt) -> ABC=DCM(CgC)
Có T/G ABC=DCM -> Góc D=BAM(2 góc tương ứng )mà 2 góc Sole trong -> AB//DC
C) Xét T/G BFM và CEM có CM=MB(GT) E3=F4=90 độ M4=M3 ( đối đỉnh) -> BFM=CEM(g.c.g)
-> ME=MF -> M là trung điểm EF
A B C M D E F
a, Xét t/g ABM và t/g DCM có:
AM=DM(gt)
BM=CM(gt)
góc AMB=góc DMC (đối đỉnh)
=>t/g ABM=t/g DCM (c.g.c)
b, Vì t/g ABM=t/g DCM (cmt) => góc ABM = góc DCM (2 góc t/ứ)
Mà 2 góc này là cặp góc so le trong
=> AB//DC
c, Xét t/g BEM và t/g CFM có:
góc BEM = góc CFM = 90 độ (gt)
BM=CN(gt)
góc BME = góc CMF (đối đỉnh)
=>t/g BEM = t/g CFM (cạnh huyền - góc nhọn)
=>EM=FM (2 cạnh t/ứ)
=>M là trung điểm của EF

PMNIEFKH
a) Xét \(\Delta PIM;\Delta PIN\) có :
\(PM=PN\) (tam giác MNP cân tại P)
\(\widehat{MPI}=\widehat{NPI}\) (PI là tia phân giác của \(\widehat{MPN}\) )
\(PI:chung\)
=> \(\Delta PIM=\Delta PIN\left(c.g.c\right)\)
*Cách khác :
Xét \(\Delta PIM;\Delta PIN\) có :
\(\widehat{PMI}=\widehat{PNI}\) (tam giác MNP cân tại P)
\(PM=PN\)(tam giác MNP cân tại P)
\(\widehat{MPI}=\widehat{NPI}\) (PI là tia phân giác của góc MPN)
=> \(\Delta PIM=\Delta PIN\left(g.c.g\right)\)
b) Xét \(\Delta PEI;\Delta PFI\) có :
\(\widehat{PEI}=\widehat{PFI}\left(=90^{^O}\right)\)
\(PI:Chung\)
\(\widehat{EPI}=\widehat{FPI}\left(cmt\right)\)
=> \(\Delta PEI=\Delta PFI\) (cạnh huyền - góc nhọn)
=> \(IE=IF\) (2 cạnh tương ứng)
c) Ta chứng minh được \(\Delta PIK=\Delta PIH\left(g.c.g\right)\)
Suy ra : \(PK=PH\) (2 cạnh tương ứng)
Xét \(\Delta PHK\) có :
\(PK=PH\left(cmt\right)\)
=> \(\Delta PHK\) cân tại P (đpcm)
d) Xét \(\Delta PEF\) cân tại E có :
\(\widehat{PEF}=\widehat{PFE}=\dfrac{180^o-\widehat{P}}{2}\left(1\right)\)
Xét \(\Delta PKH\) cân tại P (cmt) có :
\(\widehat{PKH}=\widehat{PHK}=\dfrac{180^o-\widehat{P}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{PEF}=\widehat{PKH}\left(=\dfrac{180^o-\widehat{P}}{2}\right)\)
Mà thấy : 2 góc này đều ở vị trí đồng vị
=> \(\text{EF // HK (đpcm)}\)

M N P E F K I
Giải:
a) Xét \(\Delta IMN,\Delta IPK\) có:
\(IN=IK\left(gt\right)\)
\(\widehat{NIM}=\widehat{PIK}\) ( đối đỉnh )
\(IM=IP\left(=\frac{1}{2}MP\right)\)
\(\Rightarrow\Delta IMN=\Delta IPK\left(c-g-c\right)\)
\(\Rightarrowđpcm\)
b) Vì \(\Delta IMN=\Delta IPK\)
\(\Rightarrow MN=PK\) ( cạnh t/ứng )
\(\Rightarrowđpcm\)
c) Vì \(\Delta IMN=\Delta IPK\)
\(\Rightarrow\widehat{NMI}=\widehat{KPI}\)
hay \(\widehat{EMI}=\widehat{FPI}\)
Xét \(\Delta IEM,\Delta IFP\) có:
\(\widehat{EMI}=\widehat{FPI}\left(cmt\right)\)
\(IM=IP\left(=\frac{1}{2}MP\right)\)
\(\widehat{EIM}=\widehat{FIP}\) ( đối đỉnh )
\(\Rightarrow\Delta IEM=\Delta IFP\left(g-c-g\right)\)
\(\Rightarrow\widehat{MEI}=\widehat{PFI}\)
\(\Rightarrow\widehat{PFI}=90^o\)
\(\Rightarrow IF\perp KP\left(đpcm\right)\)
Vậy...