Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Vì HD vuông góc với AB
=> HDB = HDA = 90 độ
Mà BAC = 90 độ (gt)
=> BAC = BDH = 90 độ
Mà 2 góc này ở vị trí đồng vị
=> DH //AE
=> DHEA là hình thang
Mà HE vuông góc với AC
=> HEA = 90 độ
=> HEA = BAC = 90 độ
=> DHEA là hình thang cân
=> DE = AH ( hình thang cân hai đường chéo bằng nhau)
=> dpcm
hình bạn tự vẽ nhé
hơi tắt nhưng chắc bạn hiểu
gọi AH giao với ED=O
ta dễ dàng có \(OE=OH;EM=MH\)
=> \(\hept{\begin{cases}\widehat{OEH}=\widehat{OHE}\\\widehat{MEH}=\widehat{MHE}\end{cases}}\)
=> \(\widehat{MED}=\widehat{MHO}=90^o\)
tương tự ta có \(\widehat{EDN}=90^o\)
=> EM//DN(cùng vuông góc với ED=> DEMN là hình thang
Mà \(\widehat{EDN}=90^o\)
=> DEMN là hình thang vuông (ĐPCM)
- Xét \(\Delta BEH\)vuông tại E (vì EH vuông góc với AB)
có EM là đường trung tuyến
suy ra BM = ME = MH
- Xét \(\Delta EMH\)có EM = MH (cmt) suy ra \(\Delta EMH\)cân tại M
suy ra \(\widehat{MEH}=\widehat{MHE}\) \(\left(1\right)\)
- Ta có: HE vuông góc với AE (gt) và AD vuông góc với AE (gt)
suy ra EH // AD
suy ra EHDA là hình thang
- Ta lại có: AE vuông góc với AD (gt) và HD vuông góc với AD (gt)
suy ra AE // HD
- Xét hình thang EHDA có EA // HD (cmt) và EH // AD (cmt)
suy ra EA = HD và EH = AD
- Dễ thấy \(\Delta AHE=\Delta DEH\)(c.g.c)
suy ra \(\widehat{HED}=\widehat{EHA}\) \(\left(2\right)\)
- Cộng \(\left(1\right)\)và \(\left(2\right)\)theo từng vế,
ta được: \(\widehat{MEH}+\widehat{HED}=\widehat{MHE}+\widehat{EHA}=90^0\)
suy ra ME vuông góc với ED
- chứng minh tượng tự ND vuông góc với ED
mà ME vuông góc với ED
suy ra ND // ME
- Xét tứ giác EMND có ND // ME
suy ra EMND là hình thang
mà \(\widehat{MED}=90^0\) suy ra (đpcm)
1a) A=D=E=90 độ
=>AEHD là hcn
=>AH=DE
b)Xét tam giác DBH vuông tại D có:
DI là đường trung tuyến ứng với cạnh huyền BH
=>DI=BH/2=IH
=>tam giác IDH cân tại I
=>góc IDH=góc IHD (1)
Gọi O là gđ 2 đường chéo AH và DE
=>OD=OA=OE=OH (tự c/m)
=> tam giác DOH cân tại O
=> góc ODH=góc OHD(2)
từ (1) và (2) => góc ODH+góc IDH=90 độ(EHD+DHI=90 độ)
=>IDvuông góc DE(3)
Cmtt ta được: KEvuông góc DE(4)
Từ (3)và (4) => DI//KE.
2a) Ta có góc HAB+góc HAC=90 độ (1)
Xét tam giác ABC vuông tại A có
AM là đg trung tuyến ứng vs cạnh huyền BC
=>AM=MC
=>tam giác AMC cân
=>góc MAC=góc ACM
Lại có: góc HAC+góc ACH=90 độ(2)
Từ (1) và (2) => góc BAH=góc ACM
Mà góc AMC=góc MAC(cmt)
=>ABH=MAC(3)
b)A=D=E=90 độ
=>AFHE là hcn
Gọi O là gđ EF và AM
OA=OF(tự cm đi nha)
=>tam giác OAF cân
=>OAF=OFA(4)
Ta có : OAF+MCA=90 độ(5)
Từ (3)(4) và (5)
=>MAC+OFA=90 độ
Hay AM vuông góc EF
k giùm mình nha.
a: Xét tứ giác ADHE co
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: ΔABC vuông tại A
mà AM là trung tuyến
nên AM=BM=CM
ADHE là hình chữ nhật
nên góc AEH=góc ADH=góc ABC
=>góc AEH+góc MAC=90 độ
=>DE vuông góc với AM
A B C H D E O P Q
câu a, dễ thấy tứ giác AEHD có 3 góc A=E=D=90 độ nên AEHD là hình chữ nhật, do đó AH=DE.
b.Xét tam giác BHD vuông tại D và có P là trung điểm BH do đso
\(\widehat{PDH}=\widehat{PHD}\)mà \(\widehat{PHD}=\widehat{QCE}\)( đồng vị)
và \(\widehat{QCE}=\widehat{QEC}\)
do đó ta có \(\widehat{PDH}=\widehat{QEC}\) mà HD//CE nên DP //QE . do đó DEPQ là hình thang
A B C I H D E O K
Cm:a) Xét tứ giác ADHE có \(\widehat{A}=\widehat{ADH}=\widehat{HEA}=90^0\)
=> ADHE là hình chữ nhật
đt DE cắt đt AH tại O
=> OA = OE
b) Ta có: OA = OE => t/giác AOE cân tại O => \(\widehat{OAE}=\widehat{OEA}\) hay \(\widehat{HAC}=\widehat{DEA}\)
Ta lại có: t/giác ABC vuông tại A => \(\widehat{B}+\widehat{C}=90^0\)
t/giác AHC vuông tại A => \(\widehat{HAC}+\widehat{C}=90^0\)
=> \(\widehat{B}=\widehat{HAC}\)
mà \(\widehat{HAC}=\widehat{DEA}\)
=> \(\widehat{ABC}=\widehat{AED}\)(đpcm)
c) Gọi K là giao điểm của AI và DE
Xét t/giác ABC vuông tại A có AI là đường trung tuyến (BI = IC)
=> AI = IB = IC = 1/2BC
=> t/giác AIC cân tại I
=> \(\widehat{IAC}=\widehat{C}\) hay \(\widehat{KAE}=\widehat{C}\)
Ta có: \(\widehat{B}+\widehat{C}=90^0\)
mà \(\widehat{B}=\widehat{KEA}\) (cmt); \(\widehat{C}=\widehat{KAE}\)(Cmt)
=> \(\widehat{KAE}+\widehat{KEA}=90^0\)
Xét t/giác AKE có \(\widehat{KAE}+\widehat{KEA}=90^0\) => \(\widehat{AKE}=90^0\)
=> AI \(\perp\)DE
a) Xét tứ giác ADHE
Ta có: góc A=900(gt)
góc ADH=900(gt)
góc EHD=900(gt)
=>tứ giác ADHE là hcn
=>AH=DE(đpcm)
a. Tứ giác AEHD có 3 góc vuông => AEHD là hình chữ nhật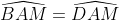
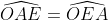hay 
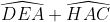(1) 
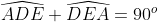( Hệ quả định lý tổng 3 góc của 1 tam giác ) (2) 
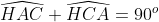(3) 
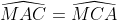hay
=> DE = AH
b.* Vì D thuộc AB =>
* Gọi O là giao của DE và AH
AEHD là hình chữ nhật => OA = OE => Tam giác OAE cân =>
Có :
Tương tự có :
Từ (1),(2),(3) => đpcm
c. GỌi K là giao của DE và AM
M là trung điểm của cạnh huyền BC trong tam giác ABC vuông tại A => AM là trung tuyến => AM = MC => Tam giác MAC cân =>
Mà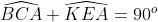
(theo (3))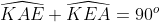 
=>
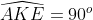
Áp dụng định lý tổng 3 góc của 1 tam giác tính được :
=> đpcm
P/s: Tham khảo nhé, mà hình như đề thiếu thì phải??
ban giai ki hon duoc ko