Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình tự vẽ nha
a, Xét ΔΔABH vuông tại H có :
AB2AB2 = HA2HA2 + BH2BH2 ( theo định lí Pytago )
AB2AB2 = 6262 + 4242 = 52 ( cm )
Chứng minh tương tự ta được AC = 117 ( cm )
Ta có : AB2AB2 = 52 cm
AC2AC2 = 117 cm
BC2BC2 = 169 cm
Mà AB2AB2 + AC2AC2 = 169 ⇒⇒ BC2BC2 = AB2AB2 + AC2AC2
⇒⇒ ΔABCΔABC vuông tại A
Vậy ΔABCΔABC vuông tại A

Câu hỏi của nguyen anh ngoc ly - Toán lớp 7 - Học toán với OnlineMath

a) xét tam giác AHB và tam giác AHD ta có
AH=AH ( cạnh chung)
BH=HD(gt)
góc AHB= góc AHD (=90)
-> tam giác AHB= tam giác AHD (c-g-c)
b) ta có
DE vuông góc AC (gt)
AB vuông góc AC ( tam giác ABC vuông tại A)
-> DE//AB
ta có
AC>AB (gt)
-> góc ABC > góc ACB ( quan hệ cạnh góc đối diện trong tam giác)
c) Xét tam giác AHB và tam giác IHD ta có
AH=HI (gt)
BH=HD(gt)
góc AHB= góc IHD (=90)
-> tam giac AHB = tam giác IHD (c-g-c)
-> góc BAH= góc HID ( 2 góc tương ứng )
mà 2 góc nẳm ở vị trí sole trong
nên BA//ID
ta có
BA//ID (cmt)
BA//DE (cm b)
-> ID trùng DE
-> I,E,D thẳng hàng

1:
a:
góc DAB+góc CAE=180 độ-góc BAE=90 độ
góc DAB+góc DBA=90 độ
=>góc DBA=góc CAE
Xét ΔDBA vuông tại D và ΔEAC vuông tại E có
BA=AC
góc DBA=góc EAC
=>ΔDBA=ΔEAC
b: ΔDBA=ΔEAC
=>DB=EA và DA=EC
BD+CE
=CA+AD
=CD

mấy bạn phải giải cho mình trước để mình xem đúng hay ko thì mình mới tick được chứ mình ko thể tick đúng lung tung được

Hình tự vẽ
+) Xét \(\Delta ABC\) vuông tại A có
\(\widehat{B}+\widehat{ACB}=90^o\) ( tính chất tam giác vuông)
\(\Rightarrow60^o+\widehat{ACB}=90^o\)
\(\Rightarrow\widehat{ACB}=30^o\)
\(\Rightarrow\widehat{ABC}>\widehat{ACB}\) ( do \(60^o>30^o\) )
\(\Rightarrow AC>AB\) (Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)
+) Xét \(\Delta ABH\) vuông tại H ta có
\(\widehat{B}+\widehat{HAB}=90^o\) ( tính chất tam giác vuông)
\(\Rightarrow60^o+\widehat{HAB}=90^o\)
\(\Rightarrow\widehat{HAB}=30^o\)
+) Ta có AH nằm giữa AC và AB ( chỗ này mk ko bt lí giải)
\(\Rightarrow\widehat{HAB}+\widehat{HAC}=\widehat{BAC}\)
\(\Rightarrow\widehat{HAC}+30^o=90^o\)
\(\Rightarrow\widehat{HAC}=90^o-30^o=60^o\)
\(\Rightarrow\widehat{HAC}< \widehat{HAB}\) ( do \(60^o>30^o\))
\(\Rightarrow CH< HB\) (Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)
b) Ta có điểm D thuộc tia đối tia HA (gt)
Mà AH \(\perp\) BC
\(\Rightarrow HD\perp\) BC
\(\Rightarrow\widehat{DHC}=\widehat{AHC}\left(=90^o\right)\)
+) Xét \(\Delta AHC\) vuông tại H và \(\Delta DHC\) vuông tại H có
HC: cạnh chung
\(\widehat{DHC}=\widehat{AHC}\) (cmt)
AH = HD ( gt)
=> \(\Delta AHC\)= \(\Delta DHC\) ( c- g-c)
c) +) Theo câu b, ta có \(\Delta AHC\)= \(\Delta DHC\)
\(\Rightarrow\widehat{ACH}=\widehat{DCH}\) ( 2 cạnh tương ứng)
và AC = AD ( 2 cạnh tương ứng)
+) Xét \(\Delta DBC\) và \(\Delta ABC\) có
BC : cạnh chung
\(\widehat{DCH}=\widehat{ACH}\) ( cmt)
AD = AC (cmt)
\(\Rightarrow\Delta DBC=\Delta ABC\) ( c-g-c)
\(\Rightarrow\widehat{BDC}=\widehat{BAC}=90^o\) ( 2 cạnh tương ứng)
~ Học tốt

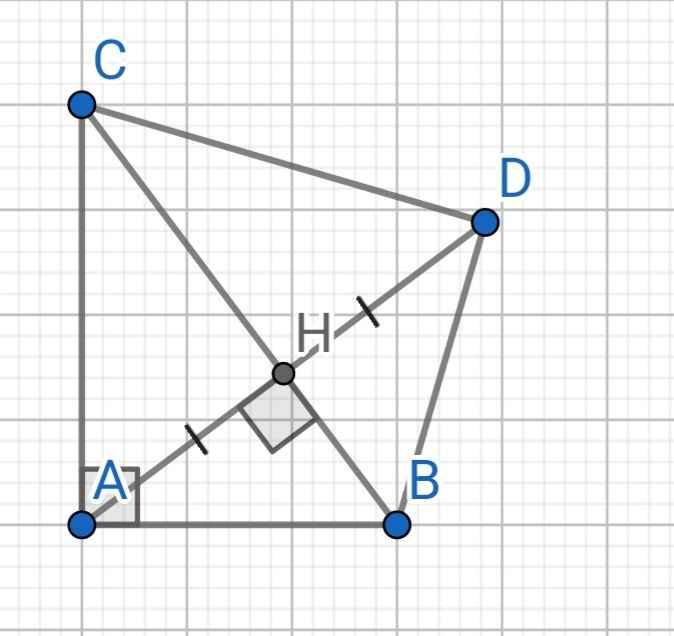 a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
BH là cạnh chung
HA = HD (gt)
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
⇒ BH là tia phân giác của ∠ABD
b) Do ∆ABH = ∆DBH (cmt)
⇒ AB = DB (hai cạnh tương ứng)
Do ∠ABH = ∠DBH (cmt)
⇒ ∠ABC = ∠DBC
Xét ∆ABC và ∆DBC có:
AB = DB (cmt)
∠ABC = ∠DBC (cmt)
AC là cạnh chung
⇒ ∆ABC = ∆DBC (c-g-c)
c) Do ∆ABC = ∆DBC (cmt)
⇒ ∠BAC = ∠BDC = 90⁰ (hai góc tương ứng)
⇒ BD ⊥ CD
\(HD=HA\)nha mọi người ko phải \(HD-HA\)nha ! giúp mình với
Ta có: AB < AC => AH < HC ( quan hệ đường xiên và hình chiếu )
=> HD = HA
=> HD < HC ; D khác A ; D thuộc AC
=> D nằm giữa H và C