Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔCDB có
Q là trung điểm của CD
P là trung điểm của BC
Do đó:QP là đường trung bình
=>QP//DB và QP=DB/2(1)
Xét ΔEDB có
M là trung điểm của ED
N là trung điểm của EB
Do đó: MN là đường trung bình
=>MN//DB và MN=DB/2(2)
Từ (1) và (2) suy ra QP//MN và QP=MN
Xét ΔDEC có
M là trung điểm của ED
Q là trung điểm của CD
Do đó: MQ là đường trung bình
=>MQ//EC
=>MQ//AC
=>MQ\(\perp\)AB
=>MQ\(\perp\)QP
Xét tứ giác MNPQ có
QP//MN
QP=MN
Do đó: MNPQ là hình bình hành
mà \(\widehat{MQP}=90^0\)
nên MNPQ là hình chữ nhật
Suy ra: MP=NQ

Tham khảo:
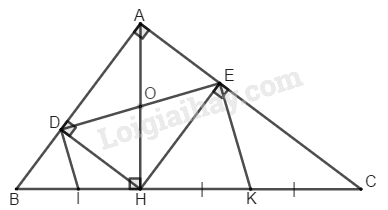
\(\Rightarrow\) Tứ giác \(DIEK\) là hình thang (định nghĩa hình thang) (đpcm).
Hình thang vuông là hình thang chỉ có 1 góc vuông thôi nhưng trong tứ giác \(DIEK\) có tận 2 góc vuông nên mình nghĩ chỉ suy ra là hình thang thôi.
Chúc bạn học tốt!

Xét ΔDCB có
Q là trung điểm của DC
P là trung điểm của BC
Do đó: QP là đường trung bình
=>QP//DB và QP=DB/2(1)
Xét ΔEDB có
M là trung điểm của ED
N là trung điểm của EB
Do đó: MN là đường trung bình
=>MN//DB và MN=DB/2(2)
Từ (1) và (2)suy ra MN//PQ và MN=PQ
Xét ΔDEC có
M là trung điểm của ED
Q là trung điểm của CD
Do đó: MQ là đường trung bình
=>MQ//EC
=>MQ//AC
=>MQ\(\perp\)AB
=>MQ\(\perp\)QP
Xét tứ giác MNPQ có
MN//PQ
MN=PQ
Do đó: MNPQ là hình bình hành
mà \(\widehat{MQP}=90^0\)
nên MNPQ là hình chữ nhật
SUy ra: MP=NQ

a: Xét ΔABM vuông tại M và ΔACN vuông tại N có
góc A chung
Do đo: ΔABM đồng dạng với ΔACN
Suy ra:AM/AN=AB/AC
hay AM/AB=AN/AC
Xét ΔAMN và ΔABC có
AM/AB=AN/AC
góc A chung
Do đo: ΔAMN đồng dạng với ΔABC
b: 