Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có \(DE\parallel BC\Rightarrow\triangle ADE\approx\triangle ABC\Rightarrow\frac{A D}{A B}=\frac{A E}{A C}\). Lại có \(EF\parallel CD\Rightarrow\triangle AFE\approx\triangle ADC\Rightarrow\frac{A F}{A D}=\frac{A E}{A C}\). Suy ra \(\frac{A F}{A D} = \frac{A D}{A B}\). Thay số: \(\frac{9}{A D} = \frac{A D}{16} \Rightarrow A D^{2} = 144 \Rightarrow A D = 12 \textrm{ } \text{cm}\).
Xét ΔADC có FE//DC
nên \(\frac{AF}{AD}=\frac{AE}{AC}\) (1)
Xét ΔABC có DE//BC
nên \(\frac{AD}{AB}=\frac{AE}{AC}\) (2)
Từ (1),(2) suy ra \(\frac{AF}{AD}=\frac{AD}{AB}\)
=>\(AF\cdot AB=AD^2\)
=>\(AD^2=9\cdot16=144=12^2\)
=>AD=12(cm)
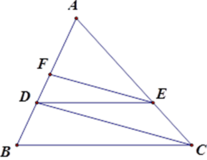
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F . A B = A D 2
Vậy 9.16 = A D 2 ó A D 2 = 144 ó AD = 12
Đáp án: C
Chọn B
Chọn đáp án B
Xét tam giác \(ADC\) có \(EF//DC\), theo định lí Thales ta có:
\(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}}\) (1)
Xét tam giác \(ABC\) có \(DE//BC\), theo định lí Thales ta có:
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) (2)
Từ (1) và (2) suy ra,
\(\frac{{AF}}{{AD}} = \frac{{AD}}{{AB}} \Rightarrow AF.AB = A{D^2} \Leftrightarrow 9.25 = A{D^2} \Rightarrow AD = \sqrt {9.25} = 15\)
Xét tam giác \(ADC\) có \(EF//DC\), theo hệ quả định lí Thales ta có:
\(\frac{{AF}}{{AD}} = \frac{{EF}}{{DC}} \Rightarrow \frac{9}{{15}} = \frac{{12}}{{DC}} \Leftrightarrow DC = \frac{{12.15}}{9} = 20\)
Vậy \(DC = 20cm\).