Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )

vẽ hình lỗi nên ko vẽ được
a) xét \(\Delta BAM\)VÀ\(\Delta CDM\)CÓ
AM=MD(GT)
\(\widehat{BMA}=\widehat{CMD}\left(Đ^2\right)\)
BM=CM (GT)
=>\(\Delta BAM\)=\(\Delta CDM\)(C-G-C)
=> ab=cd( hai cạnh tương ứng )
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\)HAY\(\widehat{ABC}=\widehat{DCB}\)( hai góc trương ứng)
MÀ HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG = NHAU
\(\Rightarrow AB//CD\left(đpcm\right)\)
xét \(\Delta BDM\)VÀ\(\Delta CAM\)CÓ
\(BM=CM\left(GT\right)\)
\(\widehat{BMD}=\widehat{CMA}\left(Đ^2\right)\)
\(DM=AM\left(GT\right)\)
=>\(\Delta BDM\)=\(\Delta CAM\)(C-G-C)
=> BD=AC ( HAI CẠNH TƯƠNG ỨNG )
\(\Rightarrow\widehat{MBD}=\widehat{MCA}\)HAY\(\widehat{CBD}=\widehat{BCA}\)( HAI GÓC TƯƠNG ỨNG )
HAI GÓC NÀY Ở VỊ TRÍ S SOLE TRONG BẰNG NHAU
=>AC//BD
B) đề sai

a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )

a)
*Chứng minh AB//CD và AB=CD
Xét ΔAMB và ΔDMC có
AM=DM(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
BM=CM(AM là đường trung tuyến ứng với cạnh BC trong ΔABC)
Do đó: ΔAMB=ΔDMC(c-g-c)
⇒\(\widehat{ABM}=\widehat{DCM}\)(hai góc tương ứng)
mà \(\widehat{ABM}\) và \(\widehat{DCM}\) là hai góc ở vị trí so le trong
nên AB//CD(dấu hiệu nhận biết hai đường thẳng song song)(đpcm1)
Ta có: ΔABM=ΔDCM(cmt)
⇒AB=CD(hai cạnh tương ứng)(đpcm2)
*Chứng minh AC//BD và AC=BD
Xét ΔAMC và ΔDMB có
AM=DM(gt)
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
CM=BM(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
Do đó: ΔAMC=ΔDMB(c-g-c)
⇒\(\widehat{MAC}=\widehat{MDB}\)(hai góc tương ứng)
mà \(\widehat{MAC}\) và \(\widehat{MDB}\) là hai góc ở vị trí so le trong
nên AC//BD(dấu hiệu nhận biết hai đường thẳng song song)(đpcm3)
Ta có: ΔAMC=ΔDMB(cmt)
⇒AC=BD(hai cạnh tương ứng)(đpcm4)

(tự vẽ hình )
câu 4:
a) có AB2 + AC2 = 225
BC2 = 225
Pytago đảo => \(\Delta ABC\)vuông tại A
b) Xét \(\Delta MAB\)và \(\Delta MDC\)
MA = MD (gt)
BM = BC ( do M là trung điểm của BC )
\(\widehat{AMB}=\widehat{CMD}\)( hai góc đối đỉnh )
=> \(\Delta MAB\)= \(\Delta MDC\) (cgc)
c) vì \(\Delta MAB\)= \(\Delta MDC\)
=> \(\hept{\begin{cases}AB=DC\\\widehat{MAB}=\widehat{MDC}\end{cases}}\)
=> AB// DC
lại có AB \(\perp\)AC => DC \(\perp\)AC => \(\Delta KCD\)vuông tại C
Xét \(\Delta\) vuông ABK và \(\Delta\)vuông KCD:
AB =CD (cmt)
AK = KC ( do k là trung điểm của AC )
=> \(\Delta\)vuông AKB = \(\Delta\)vuông CKD (cc)
=> KB = KD
d. do KB = KD => \(\Delta KBD\)cân tại K
=> \(\widehat{KBD}=\widehat{KDB}\)(1)
có \(\Delta ADC\)vuông tại C => \(AD=\sqrt{AC^2+DC^2}=15\)
=> MD = 7.5
mà MB = 7.5
=> MB = MD
=> \(\Delta MBD\)cân tại M
=> \(\widehat{MBD}=\widehat{MDB}\)(2)
Từ (1) và (2) => \(\widehat{KBD}-\widehat{MBD}=\widehat{KDB}-\widehat{MDB}\)hay \(\widehat{KBM}=\widehat{KDM}\)
Xét \(\Delta KBI\)và \(\Delta KDN\)có:
\(\widehat{KBI}=\widehat{KDN}\)(cmt)
\(\widehat{KBD}\)chung
KD =KB (cmt)
=> \(\Delta KBI\)= \(\Delta KDN\)(gcg)
=> KN =KI
=. đpcm
câu 5:
a) Xét \(\Delta ABM\)và \(\Delta MDC\):
MA=MD(gt)
MB=MC (M là trung điểm của BC)
\(\widehat{BMA}=\widehat{DMC}\)( đối đỉnh )
=> \(\Delta BMA=\Delta CMD\)(cgc)
b) Xét \(\Delta\)vuông ABC
có AM là đường trung tuyến của tam giác
=> \(AM=\frac{1}{2}BC\)mà \(BM=MC=\frac{1}{2}BC\)(do M là trung điểm của BC )
=> AM = BM = MC
có MA =MD => AM = MD =MB =MC
=> BM +MC = AM +MD hay BC =AD
Xét \(\Delta BAC\)và \(\Delta DCA\)
AB =DC
AC chung
BC =DC
=> \(\Delta BAC\)= \(\Delta DCA\)(ccc)
c. Xét \(\Delta ABM\)
BM=AM
\(\widehat{ABM}\)= 600
=> đpcm


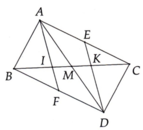
a.
Xét \(\Delta AMB\) và \(\Delta DMC\) ; có :
\(MA=MD\left(gt\right)\\ \widehat{AMB}=\widehat{DMC}\left(đ^2\right)\\ MB=MC\\ \Rightarrow\Delta AMB=\Delta DMC\left(c-g-c\right)\\ \Rightarrow AB=CD;\widehat{MAB}=\widehat{MDC}\\ \widehat{MAB}=\widehat{MDC}\)
=> AB // CD
TT : AC// BD ; AC=BD
b.
Có vấn đề chỗ BF cắt BC tại K ; !!
coi lại đề