Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D F E H Ta có : \(\dfrac{HD}{AD}=\dfrac{S_{HBC}}{S_{ABC}}\)( Do có chung đáy BC nên tỉ số hai đường cao bằng tỉ số hai diện tích) ( *)
Tương tự , ta có : \(\dfrac{HE}{BE}=\dfrac{S_{HAC}}{S_{ABC}}\) (**) Và \(\dfrac{HF}{CF}=\dfrac{S_{HAB}}{S_{ABC}}\)(***)
Từ ( *; **; ***) Ta có được :
\(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{HAC}+S_{HBC}+S_{HAB}}{S_{ABC}}=\dfrac{S_{ABC}}{S_{ABC}}=1\)

A B C D E F H
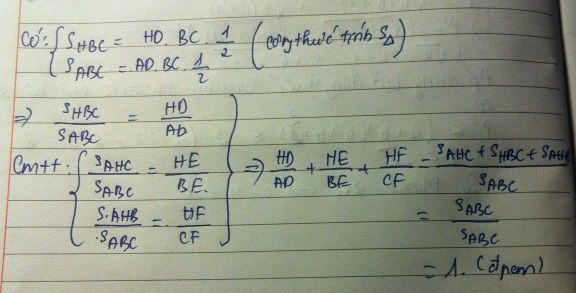
Ta có: \(\dfrac{AD.BC}{2}=S_{ABC}\Rightarrow AD=\dfrac{2S_{ABC}}{BC}\)
\(\Rightarrow\dfrac{HD}{AD}=\dfrac{HD.BC}{2S_{ABC}}\)
Tương tự: \(\dfrac{HE}{BE}=\dfrac{HE.AC}{2S_{ABC}};\dfrac{HF}{CF}=\dfrac{HF.AB}{2S_{ABC}}\)
\(\Rightarrow\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{BHC}+S_{AHC}+S_{AHC}}{S_{ABC}}=1\)

Lời giải:
câu c)
Ta có: \(\frac{HD}{AD}=\frac{HD.BC}{AD.BC}=\frac{2S_{BHC}}{2S_{ABC}}=\frac{S_{HBC}}{S_{ABC}}\)
\(\frac{HE}{BE}=\frac{HE.AC}{BE.AC}=\frac{2S_{AHC}}{2S_{ABC}}=\frac{S_{AHC}}{S_{ABC}}\)
\(\frac{HF}{CF}=\frac{HF.AB}{CF.AB}=\frac{2S_{AHB}}{2S_{ABC}}=\frac{S_{AHB}}{S_{ABC}}\)
Cộng theo vế các đẳng thức vừa thu được:
\(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\frac{S_{HBC}+S_{AHC}+S_{AHB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Ta có đpcm.

a: Xét ΔDBH vuông tại D và ΔDAC vuông tại D có
góc DBH=góc DAC
Do đó: ΔDBH đồng dạng với ΔDAC
Suy ra: DB/DA=DH/DC
hay \(DB\cdot DC=DH\cdot DA\)
b: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
Do đó: ΔAEB đồng dạng với ΔAFC
Suy ra: AE/AF=AB/AC
hay AE/AB=AF/AC
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
Do đó: ΔAEF đồng dạng với ΔABC
d: Ta có: góc EFH=góc DAC
góc DFH=góc EBC
mà góc DAC=góc EBC
nên góc EFH=góc DFH
hay FH là phân giác của góc EFD
Ta có: góc FEH=góc BAD
góc DEH=góc DCH
mà góc DCH=góc BAD
nên góc FEH=góc DEH
hay EH là phân giác của góc FED
Xét ΔFED có
EH là phân giác
FH là phân giác
Do đó: H là tâm đường tròn nội tiếp ΔEFD

b: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
góc EBC chug
Do đo: ΔBDH đồng dạng với ΔBEC
=>BD/BE=BH/BC
=>BH*BE=BD*BC
Xét ΔCDH vuông tại D và ΔCFB vuông tại F có
góc FCB chung
Do đó; ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CD*CB=CH*CF
BH*BE+CH*CF=BD*BC+CD*CB=BC^2
c: góc HED=góc HCD
góc HEF=góc BAD
mà góc HCD=góc BAD
nên góc HED=góc HEF
=>EH là phân giác của góc FED(1)
góc EFH=góc DAC
góc DFH=góc EBC
mà góc DAC=góc EBC
nên góc EFH=góc DFH
=>FH là phân giác của góc EFD(2)
Từ (1), (2) suy ra H là tâm đường tròn nội tiếp ΔEFD
=>H cách đều ba cạnh của ΔFED