K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

T
1 tháng 8 2019
A B C D E M N I K
Dễ chứng minh I là trung điểm BD, K là trung điểm CE.
Ta có tính chất: Trong hình thang, đoạn thẳng nối trung điểm hai đường chéo song song với hai đáy và có độ dài bằng nửa hiệu độ dài hai đáy. (chưa nghĩ ra cách chứng minh)
Do đó xét hình thang BEDC có I và K là trung điểm hai đường chéo nên
\(IK=\frac{BC-ED}{2}=\frac{BC-\frac{1}{2}BC}{2}=\frac{\frac{1}{2}BC}{2}=\frac{1}{4}BC=\frac{a}{4}\)
Từ từ nghĩ cách chứng minh tính chất trên nha!
từ A kẻ Ax //BC cắt BK tại F

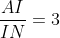
) nên KI //MN
nên KI //MN

vì AF//BC nên
do đó AFCB là hình bình hành
vì AF //BM nên
tương tự
do đó
Ứng dụng giải toán đã được review rất hay bởi trang báo uy tín https://www.facebook.com/docbaoonlinethayban/videos/467035000526358/?v=467035000526358 Cả nhà tải ngay bằng link dưới đây nhé. https://giaingay.com.vn/downapp.html