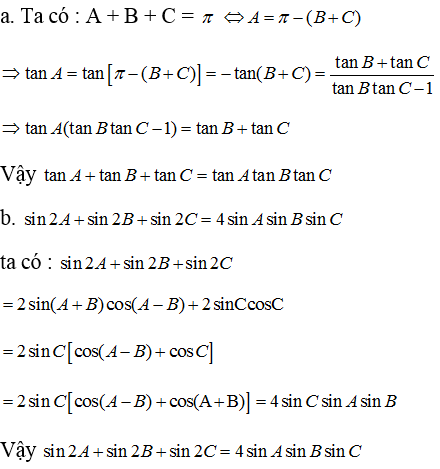Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f/
\(sin2A+sin2B+sin2C=2sin\left(A+B\right).cos\left(A-B\right)+2sinC.cosC\)
\(=2sinC.cos\left(A-B\right)+2sinC.cosC\)
\(=2sinC\left(cos\left(A-B\right)+cosC\right)\)
\(=2sinC\left[cos\left(A-B\right)-cos\left(A+B\right)\right]\)
\(=4sinC.sinA.sinB\)
g/
\(cos^2A+cos^2B+cos^2C=\frac{1}{2}+\frac{1}{2}cos2A+\frac{1}{2}+\frac{1}{2}cos2B+cos^2C\)
\(=1+\frac{1}{2}\left(cos2A+cos2B\right)+cos^2C\)
\(=1+cos\left(A+B\right).cos\left(A-B\right)+cos^2C\)
\(=1-cosC.cos\left(A-B\right)+cos^2C\)
\(=1-cosC\left(cos\left(A-B\right)-cosC\right)\)
\(=1-cosC\left[cos\left(A-B\right)+cos\left(A+B\right)\right]\)
\(=1-2cosC.cosA.cosB\)
d/ \(sinA+sinB+sinC=2sin\frac{A+B}{2}cos\frac{A-B}{2}+2sin\frac{C}{2}.cos\frac{C}{2}\)
\(=2cos\frac{C}{2}.cos\frac{A-B}{2}+2sin\frac{C}{2}.cos\frac{C}{2}\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}+sin\frac{C}{2}\right)\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}+cos\frac{A+B}{2}\right)\)
\(=4cos\frac{C}{2}.cos\frac{A}{2}.cos\frac{B}{2}\)
e/
\(cosA+cosB+cosC=2cos\frac{A+B}{2}cos\frac{A-B}{2}+1-2sin^2\frac{C}{2}\)
\(=1+2sin\frac{C}{2}.cos\frac{A-B}{2}-2sin^2\frac{C}{2}\)
\(=1+2sin\frac{C}{2}\left(cos\frac{A-B}{2}-sin\frac{C}{2}\right)\)
\(=1+2sin\frac{C}{2}\left(cos\frac{A-B}{2}-cos\frac{A+B}{2}\right)\)
\(=1+4sin\frac{C}{2}.sin\frac{A}{2}sin\frac{B}{2}\)

\(A=\frac{2sinx.cosx+sinx}{1+2cos^2x-1+cosx}=\frac{sinx\left(2cosx+1\right)}{cosx\left(2cosx+1\right)}=\frac{sinx}{cosx}=tanx\)
\(B=\frac{cosa}{sina}\left(\frac{1+sin^2a}{cosa}-cosa\right)=\frac{cosa}{sina}\left(\frac{1+sin^2a-cos^2a}{cosa}\right)=\frac{cosa}{sina}.\frac{2sin^2a}{cosa}=2sina\)
\(C=\frac{1+cos2x+cosx+cos3x}{2cos^2x-1+cosx}=\frac{1+2cos^2x-1+2cos2x.cosx}{cos2x+cosx}=\frac{2cosx\left(cosx+cos2x\right)}{cos2x+cosx}=2cosx\)
\(D=\frac{2sinx.cosx.\left(-tanx\right)}{-tanx.sinx}-2cosx=2cosx-2cosx=0\)
\(E=cos^2x.cot^2x-cot^2x+cos^2x+2cos^2x+2sin^2x\)
\(E=cot^2x\left(cos^2x-1\right)+cos^2x+2=\frac{cos^2x}{sin^2x}\left(-sin^2x\right)+cos^2x+2=2\)
\(F=\frac{sin^2x\left(1+tan^2x\right)}{cos^2x\left(1+tan^2x\right)}=\frac{sin^2x}{cos^2x}=tan^2x\)
Câu G mẫu số có gì đó sai sai, sao lại là \(2sina-sina?\)
\(H=sin^4\left(\frac{\pi}{2}+a\right)-cos^4\left(\frac{3\pi}{2}-a\right)+1=cos^4a-sin^4a+1\)
\(=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)+1=cos^2a-\left(1-cos^2a\right)+1=2cos^2a\)

a/
\(\frac{1}{sinx}+\frac{cosx}{sinx}=\frac{1+cosx}{sinx}=\frac{1+2cos^2\frac{x}{2}-1}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{2cos^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{cos\frac{x}{2}}{sin\frac{x}{2}}=cot\frac{x}{2}\)
b/
\(\frac{1-cosx}{sinx}=\frac{1-\left(1-2sin^2\frac{x}{2}\right)}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{2sin^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{sin\frac{x}{2}}{cos\frac{x}{2}}=tan\frac{x}{2}\)
c/
\(tan\frac{x}{2}\left(\frac{1}{cosx}+1\right)=\left(\frac{1-cosx}{sinx}\right)\left(\frac{1}{cosx}+1\right)=\frac{\left(1-cosx\right)\left(1+cosx\right)}{sinx.cosx}=\frac{1-cos^2x}{sinx.cosx}\)
\(=\frac{sin^2x}{sinx.cosx}=\frac{sinx}{cosx}=tanx\)
d/
\(\frac{sin2a}{2cosa\left(1+cosa\right)}=\frac{2sina.cosa}{2cosa\left(1+2cos^2\frac{a}{2}-1\right)}=\frac{sina}{2cos^2\frac{a}{2}}=\frac{2sin\frac{a}{2}cos\frac{a}{2}}{2cos^2\frac{a}{2}}=tan\frac{a}{2}\)
e/
\(cotx+tan\frac{x}{2}=\frac{cosx}{sin}+\frac{1-cosx}{sinx}=\frac{cosx+1-cosx}{sinx}=\frac{1}{sinx}\)
Các câu c, e đều sử dụng kết quả từ câu b
f/
\(3-4cos2x+cos4x=3-4cos2x+2cos^22x-1\)
\(=2cos^22x-4cos2x+2=2\left(cos^22x-2cos2x+1\right)\)
\(=2\left(cos2x-1\right)^2=2\left(1-2sin^2x-1\right)^2\)
\(=2.\left(-2sin^2x\right)^2=8sin^4x\)
g/
\(\frac{1-cosx}{sinx}=\frac{sinx\left(1-cosx\right)}{sin^2x}=\frac{sinx\left(1-cosx\right)}{1-cos^2x}=\frac{sinx\left(1-cosx\right)}{\left(1-cosx\right)\left(1+cosx\right)}=\frac{sinx}{1+cosx}\)
h/
\(sinx+cosx=\sqrt{2}\left(sinx.\frac{\sqrt{2}}{2}+cosx.\frac{\sqrt{2}}{2}\right)\)
\(=\sqrt{2}\left(sinx.cos\frac{\pi}{4}+cosx.sin\frac{\pi}{4}\right)=\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\)
i/
\(sinx-cosx=\sqrt{2}\left(sinx.\frac{\sqrt{2}}{2}-cosx.\frac{\sqrt{2}}{2}\right)\)
\(=\sqrt{2}\left(sinx.cos\frac{\pi}{4}-cosx.sin\frac{\pi}{4}\right)=\sqrt{2}sin\left(x-\frac{\pi}{4}\right)\)
j/
\(cosx-sinx=\sqrt{2}\left(cosx.\frac{\sqrt{2}}{2}-sinx\frac{\sqrt{2}}{2}\right)\)
\(=\sqrt{2}\left(cosx.cos\frac{\pi}{4}-sinx.sin\frac{\pi}{4}\right)=\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)

a/ \(\frac{A}{2}+\left(\frac{B}{2}+\frac{C}{2}\right)=90^0\)
\(\Rightarrow sin\frac{A}{2}=cos\left(\frac{B}{2}+\frac{C}{2}\right)=cos\frac{B}{2}cos\frac{C}{2}-sin\frac{B}{2}.sin\frac{C}{2}\)
b/ \(\frac{tan^2A-tan^2B}{1-tan^2A.tan^2B}=\frac{\left(tanA-tanB\right)}{\left(1+tanA.tanB\right)}.\frac{\left(tanA+tanB\right)}{\left(1-tanA.tanB\right)}=tan\left(A-B\right).tan\left(A+B\right)\)
\(=tan\left(A-B\right).tan\left(180^0-C\right)=-tan\left(A-B\right).tanC\)
c/
\(A+B+C=180^0\Rightarrow cot\left(A+B\right)=-cotC\)
\(\Leftrightarrow\frac{cotA.cotB-1}{cotA+cotB}=-cotC\)
\(\Leftrightarrow cotA.cotB-1=-cotA.cotC-cotB.cotC\)
\(\Leftrightarrow cotA.cotB+cotB.cotC+cotA.cotC=1\)