Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\widehat{BAC}=60^0\Rightarrow\widehat{BOC}=120^0\)
\(BC=\sqrt{2R^2-2R^2.\cos120^0}=R\sqrt{3}=2\sqrt{3}\left(cm\right)\)
\(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.3.2\sqrt{3}=3\sqrt{3}\left(cm^2\right)\)

A B C M 2cm 2cm 2cm
a) Vì AM là trung tuyến của \(\Delta ABC\)tại A \(\Rightarrow MB=MC\)
Vì \(\Delta ABM\)là tam giác đều có cạnh là 2cm\(\Rightarrow AB=AM=BM=2cm\)
Do đó độ dài cạnh BC là : \(2+2=4cm\)
Áp dụng định lý Py-ta-go trong tam giác vuông ABC ta được :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=4^2-2^2=16-4=12\)
\(\Rightarrow AC=\sqrt{12}\left(cm\right)\)
b) Diện tích \(\Delta ABC\)là : \(\frac{1}{2}\left(AB.AC\right)=\frac{2.\sqrt{12}}{2}=\sqrt{12}\left(cm^2\right)\)

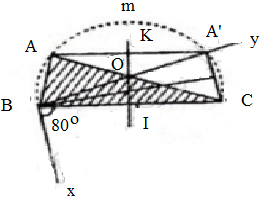
Trình tự dựng gồm các bước sau:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 80 trên đoạn thẳng BC (cung BmC).
- Trên đường vuông góc với BC tại I(I là trung điểm BC), chọn điểm K sao cho IK = 2cm. Từ K dựng đường thẳng vuông góc với IK. Đường thẳng này cắt cung chứa góc BmC tại A và A'.
ΔABC (hoặc ΔA'BC) là tam giác thỏa mãn yêu cầu đề bài.

CHO MÌNH SỬA LẠI CÂU 2: Biết chu vi \(\Delta ABH=30cm\)và chu vi \(\Delta ACH=10cm\).Tính chu vi \(\Delta ABC\)

\(\text{Hình bạn tự vẽ ^_^}\)
\(\text{a)Ta có: }AB^2=HB.BC=1,8.5=9\)
\(\Rightarrow AB=\sqrt{9}=3\left(\text{cm}\right)\)
\(\text{Lại có: }HC=BC-BH=5-1,8=3,2\left(\text{cm}\right)\)
\(\text{và: }AH^2=BH.CH=1,8.3,2=5,76\)
\(\Rightarrow AH=\sqrt{5,76}=2,4\left(\text{cm}\right)\)
\(\text{b) vì M là trung điểm BC nên }BM=CM=\frac{BC}{2}=\frac{5}{2}=2,5\left(\text{cm}\right)\)
\(\text{Ta lại có: }AC^2=CH.BC=3,2.5=16\)
\(\Rightarrow AC=\sqrt{16}=4\left(\text{cm}\right)\)
\(\text{Xét }\Delta DMC\text{ và }\Delta BAC\text{ có:}\)
\(\widehat{DMC}=\widehat{BAC}=90^o\)
\(\widehat{C}\text{ là góc chung}\)
\(\text{ }\Rightarrow\Delta DMC\text{ đồng dạng với }\Delta BAC\)
\(\Rightarrow\frac{DM}{AB}=\frac{DC}{BC}=\frac{CM}{AC}=\frac{2,5}{4}=0,625\left(\text{Tỉ số đồng dạng}\right)\)
\(\text{Vậy }\frac{S_{DMC}}{S_{BAC}}=\left(0,625\right)^2=\frac{25}{64}\)
a, \(AB=\sqrt{BH\cdot BC}=\sqrt{1,8\cdot5}=3\)
\(AH=\sqrt{AB^2-BH^2}=\sqrt{3^2-1,8^2}=2,4\)
b, \(\frac{S_{ABC}}{S_{DMC}}=\frac{MC^2}{BC^2}=\frac{1}{4}\)
c,\(\Delta ABC~\Delta MDC\Rightarrow\frac{BC}{DC}=\frac{AC}{MC}\Rightarrow AC\cdot CD=\frac{1}{2}BC^2\)
d,Cái này bạn tự tính nhá
Mk hơi lười nên làm hơi tắt có j thông cảm mk nha

A B C H O K
a) Chứng minh \(AB.AC=2R.AH\).Nối đường kính BK là thấy liền.Ta sẽ chứng minh \(\Delta ABK~\Delta HAC\).Đến đây thì Ez rùi
b)Lợi dụng câu a ta có:
\(AB.AC=2R.AH\Rightarrow AB.AC.BC=2RAH.BC=4R.SABC\)hay \(S_{ABc}=\frac{AB.BC.CA}{4R}\)

A B M C O O 1 2 O I E D N
a) Có ^AO1O2 = ^AO1M/2 = 1/2.Sđ(AM của (O1) = ^ABM = ^ABC. Tương tự ^AO2O1 = ^ACB
Suy ra \(\Delta\)AO1O2 ~ \(\Delta\)ABC (g.g) (đpcm).
b) Từ câu a ta có \(\Delta\)AO1O2 ~ \(\Delta\)ABC. Hai tam giác này có đường trung tuyến tương ứng AO,AI
Khi đó \(\Delta\)AOO1 ~ \(\Delta\)AIB (c.g.c) => \(\frac{AO}{AO_1}=\frac{AI}{AB}\). Đồng thời ^OAI = ^O1AB
=> \(\Delta\)AOI ~ \(\Delta\)AO1B (c.g.c). Mà \(\Delta\)AO1B cân tại O1 nên \(\Delta\)AOI cân tại O (đpcm).
c) Xét đường tròn (O1): ^DAM nội tiếp, ^DAM = 900 => DM là đường kính của (O1)
=> ^DBM = 900 => DB vuông góc với BC. Tương tự EC vuông góc với BC
Do vậy BD // MN // CE. Bằng hệ quả ĐL Thales, dễ suy ra \(\frac{ND}{NE}=\frac{MB}{MC}\)(1)
Áp dụng ĐL đường phân giác trong tam giác ta có \(\frac{MB}{MC}=\frac{AB}{AC}\)(2)
Từ (1) và (2) suy ra \(\frac{ND}{NE}=\frac{AB}{AC}\)=> ND.AC = NE.AB (đpcm).