Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình:
A C B D E F
Giải:
a) Xét tam giác ABC cân tại A có đường trung tuyến AE
Suy ra AE đồng thời là đường phân giác của góc CAB
\(\Rightarrow\widehat{CAE}=\dfrac{1}{2}\widehat{CAB}\)
Xét tương tự với tam giác CAD, ta được:
\(\widehat{CAF}=\dfrac{1}{2}\widehat{CAD}\)
Ta có: \(\widehat{CAB}+\widehat{CAD}=180^0\) (Hai góc kề bù)
\(\Rightarrow\widehat{CAE}+\widehat{CAF}=\widehat{EAF}\)
\(\Leftrightarrow\dfrac{1}{2}\widehat{CAB}+\dfrac{1}{2}\widehat{CAD}=\widehat{EAF}\)
\(\Leftrightarrow\dfrac{1}{2}\left(\widehat{CAB}+\widehat{CAD}\right)=\widehat{EAF}\)
\(\Leftrightarrow\dfrac{1}{2}180^0=\widehat{EAF}\)
\(\Leftrightarrow\widehat{EAF}=90^0\) (1)
b) Ta có tam giác ABC cân tại A có đường trung tuyến AE
Suy ra AE đồng thời là đường cao của góc CAB
\(\Rightarrow\widehat{AEC}=90^0\) (2)
Chứng minh tương tự với tam giác CAD, ta được:
\(\Rightarrow\widehat{AFC}=90^0\) (3)
Từ (1), (2) và (3)
Suy ra tứ giác AECF là hình chữ nhật
\(\Rightarrow AF//BC\)
\(\Rightarrow CF\perp CE\)
Mà F thuộc CD, E thuộc BC
\(\Rightarrow CD\perp BC\)
Vậy ...

Giải
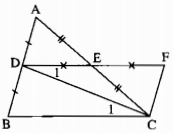
a) Xét ∆ADE và ∆CFE, ta có:
AE = CE (gt)
ˆAED = CEF^ (đối đỉnh)
DE = FE(gt)
Suy ra: ∆ADE = ∆CFE (c.g.c)
⇒⇒ AD = CF (hai cạnh tương ứng)
Mà AD = DB (gt)
Vậy: DB = CF
b) Ta có: ∆ADE = ∆CFE (chứng minh trên)
⇒ˆADE = CFE^ (2 góc tương ứng)
⇒⇒ AD // CF (vì có cặp góc so le trong bằng nhau)
Hay AB // CF
Xét ∆DBC = ∆CDF, ta có:
BD = CF (chứng minh trên)
ˆBDC = ˆFCD (hai góc so le trong vì CF // AB)
DC cạnh chung
Suy ra: ∆BDC = ∆FCD(c. g. c)
c) Ta có: ∆BDC = ∆FCD (chứng minh trên)
Suy ra: ˆC1 = ˆD1 (hai góc tương ứng)
Suy ra: DE // BC (vì có hai góc so le trong bằng nhau)
\(\Delta\)BDC = ∆FCD => BC = DF (hai cạnh tương ứng)
Mà DE = 1 : 2 . DF(gt). Vậy DE = 1 : 2 . BC
a/Xét ΔAED va ΔCEF có:
AE=CE(vì E là trung điểm của AC)
∠AED=∠CEF(đối đỉnh)
ED=EF(vì E là trung điểm của DF)
nên: ΔAED=ΔCEF(c-g-c)
do đó: AD=CF
mà AD=BD (vì D là trung điểm của AB)
vậy BD=CF
b/Ta có: ∠EAD=∠ECF(vì ΔAED=ΔCEF)
mà hai góc này ở vị trí so le trong
nên AB//CF
Ta có:AB//CF(cmt)
nên ∠BDC=∠FCD (hai góc so le trong)
Xét: ΔBDC và ΔFCD có:
DC là cạnh chung
∠BDC=∠FCD(cmt)\
DB=CF(cmt)
nên ΔBDC=ΔFCD(c-g-)
c/Ta có: ∠BCD=∠FDC(vì ΔBDC=ΔFCD)
mà hai góc này ở vị trí so le trong
nên DE//BC
Ta có: \(DE=\dfrac{1}{2}DF\)(vì E là trung điểm của DF)
mà DF=CB(vì ΔFCD=ΔBDC)
vậy \(DE=\dfrac{1}{2}CB\)
A B C F E D

Bài 4:
(Bạn tự vẽ hình theo đề bài nhé!)
Theo đề bài, ta có:
BE = \(\dfrac{1}{3}BC\) => CE = \(\dfrac{2}{3}BC\)
BA=BD => BC là đường trung tuyến ΔACD
=> E là trọng tâm ΔACD
Mà AE∩CD tại K (gt) => K là trung điểm CD => CK = DK

vì AM là trung tuyến của tam giác vuông ABC (M là trung điểm của cạnh BC)
=>AM=1/2*BC=BM=CM
xét tam giácBMA và tam giác DMC có :
AM=MD(gt)
góc BMA=góc DMC (đ đ)
BM=MC(gt)
=> 2 tam giác đó bằng nhau(c-g-c)
=>ACB=ADC(2GTU)
AB=DC(2ctu)
ta có BM+CM =BC, AM+MD=AD
mà BM=CM, AM=MD
và AM=BM=CM
=> BC=AD
xét tam giác BAC và tam giác DCA có :
BA=DC (cmt)
AC là cạnh chung
BC=AD (cmt)
=> 2 tam giác đó bằng nhau (c--c-c)=>BAC=DCA=90 độ ( 2gtu)=>DC vuông góc vs AC

ta có:
^abc + ^adc = ^chjdsk