Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét ∆ ABC có đg ttrực của AB và AC giao nhau tại O
➡️O là tâm đg tròn ngoại tiếp ∆ ABC
➡️AO là đg ttrực của BC (đpcm)
b, Gọi giao điểm của AO là BC là H.
Xét ∆ ABC cân tại A
➡️AO là đg ttrực đồng thời là đg phân giác
➡️Góc BAO = góc CAO = góc BAC ÷ 2 = 120° ÷ 2 = 60°
Vì O là tâm đg tròn ngoại tiếp ∆ ABC (cmt)
➡️OA = OB = OC
Xét ∆ ABO cân tại O (OA = OB) có góc BAO = 60°
➡️∆ ABO đều
➡️BH là đg cao đồng thời là ttuyến
➡️BH là đg ttuyến của AC
mà E là giao của ttrực AB và ttuyến AO
➡️E là trọng tâm ∆ ABO
C/m tương tự ta có F là trọng tâm ∆ ACO (đpcm)
c, Xét ∆ ABC cân tại A
Góc ABC = góc ACB = (180° - 120°) ÷ 2 = 30°
Gọi OM và ON lần lượt là đg ttrực của AB và AC
Vì AB = AC ➡️AM = BM = AN = CN
Xét ∆ vuông BEM và ∆ CFN có:
Góc M = góc N = 90°
BM = CN (cmt)
Góc ABC = góc ACB (cmt)
➡️∆ vuông BEM = ∆ vuông CFN (ch - gn)
➡️BE = CF ( 2 cạnh t/ư) (1)
ME = NF (2 cạnh t/ư)
Xét ∆ vuông BEM có góc ABC = 30°
➡️Góc BEM = 90° - 30° = 60°
mà góc BEM đối đỉnh với góc OEH
➡️Góc BEM = góc OEH = 60°
Xét ∆ OBE có góc EBO = góc EOB = 60° ÷ 2 = 30°
➡️∆ OBE cân tại E
➡️BE = OE
Ta có: OE + ME = OM
OF + NF = ON
mà OM = ON, ME = NF
➡️OE = OF
Xét ∆ OEF cân tại O (OE = OF) có góc OEH = 60°
➡️∆ OEF đều
➡️OE = EF
mà OE = BE (cmt)
➡️BE = EF (2)
Từ (1) và (2) ➡️BE = EF = CF (đpcm)
Hok tốt~
P/s : ôi mỏi tay quá k mk với~

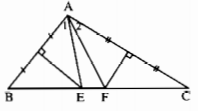
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E. Suy ra \(\widehat{B}=\widehat{A_1}\). Tương tự, có \(\widehat{C}=\widehat{A_2}\). Ta có:
\(\widehat{EAF}=\widehat{A}-\left(\widehat{A_1}+\widehat{A_2}\right)=\widehat{A}-\left(\widehat{B}+\widehat{C}\right)\)
Mặt khác
\(\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-100^0=80^0\)