Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Có 3+4+3+4+7+2+4=9 số liệu nằm trong nửa khoảng chiếm [40;8;79;2) chiếm 27 30 × 100 = 90 %
Chọn đáp án D.
Em cảm ơn 
a) ta có :
\(\Delta'=1^2-\left(-1-m\right)\left(m^2-1\right)=1-\left(-m^2+1-m^3+m\right)=1+m^2-1+m^3-m=m^3+m^2-m=m\left(m^2+m-1\right)\)để phương trình có nghiệm thì \(\Delta\ge0\)
hay \(m\left(m^2+m-1\right)\ge0\)
=> \(\left\{{}\begin{matrix}m\ge0\\m^2+m-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\ge0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2\ge\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left[{}\begin{matrix}m+\dfrac{1}{2}\ge\\m+\dfrac{1}{2}\le-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\dfrac{\sqrt{5}}{2}}\)
C1:
\(A=\dfrac{10^{50}+2}{10^{50}-1}=\dfrac{10^{50}-1}{10^{50}-1}+\dfrac{3}{10^{50}-1}=1+\dfrac{3}{10^{50}-1}\\ B=\dfrac{10^{50}}{10^{50}-3}=\dfrac{10^{50}-3}{10^{50}-3}+\dfrac{3}{10^{50}-3}=1+\dfrac{3}{10^{50}-3}\\ \text{Vì }10^{50}-3< 10^{50}-1\Rightarrow\dfrac{3}{10^{50}-3}>\dfrac{3}{10^{50}-1}\Rightarrow1+\dfrac{3}{10^{50}-3}>1+\dfrac{3}{10^{50}-1}\Leftrightarrow B>A\)
Vậy \(B>A\)
C2: Áp dụng \(\dfrac{a}{b}>1\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\left(n>0\right)\)
Dễ thấy
\(B=\dfrac{10^{50}}{10^{50}-3}>1\\ \Rightarrow B=\dfrac{10^{50}}{10^{50}-3}>\dfrac{10^{50}+2}{10^{50}-3+2}=\dfrac{10^{50}+2}{10^{50}-1}=A\)
Vậy \(B>A\)
cho đến khi màn hình hiện ra 
để lấy 4 chữ số phần thập phân. Kết quả hiện ra trên màn hình là 8183.0047.
ta thấy:\(\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\)
> áp dụng bđt cosi: 1+b2>=2b
>\(a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab^2}{2b}=a-\dfrac{ab}{2}\)
cminh tương tự với \(\dfrac{b}{1+c^2};\dfrac{c}{1+b^2}\)
cộng lần lượt 2 vế ta vừa cminh
>bthức tương đương với: a+b+c-\(\dfrac{ab+bc+ca}{2}\ge3-\dfrac{3}{2}=\dfrac{3}{2}\) đpcminh
(vì (a+b+c)2>=3(ab+bc+ca) hay 32>=3(ab+bc+ca)
> ab+bc+ca<=3)
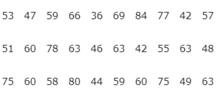
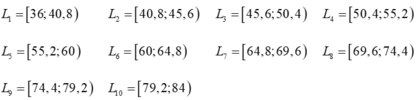
Ta có bảng phân bố tần số-tần suất ghép lớp sau: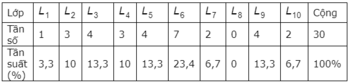
b) Có 3+4+3+4+7+2+4=27 số liệu nằm trong nửa khoảng [40,8;79,2) chiếm 27 : 30 = 90%