Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1. Ta có: Khi cộng vào mỗi số liệu của một dãy số liệu thống kê cùng một hằng số thì phương sai và độ lệch chuẩn không thay đổi. Do đó độ lệch chuẩn của dãy (2) vẫn là 2 kg.
Cách 2. Tính trực tiếp độ lệch chuẩn của dãy (2).
Đáp án: A.

Chọn D.
Dãy số trên đã được sắp xếp theo thứ tự tăng dần.
Dãy số trên có 9 phần tử. Trong dãy này số đứng giữa là 7.
⇒ Số trung vị là 7.

a) Ta có: \(8 - 7 = 1;6 - 7 = - 1;7 - 7 = 0;5 - 7 = - 2;9 - 7 = 2\)
b) +) Bình phương các độ lệch là: \({(8 - 7)^2} = 1;{(6 - 7)^2} = 1;{(7 - 7)^2} = 0;{(5 - 7)^2} = 4;{(9 - 7)^2} = 4\)
+) Trung bình cộng của bình phương các độ lệch là:
\({s^2} = \frac{{{{(8 - 7)}^2} + {{(6 - 7)}^2} + {{(7 - 7)}^2} + {{(5 - 7)}^2} + {{(9 - 7)}^2}}}{5} = 2\)

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.
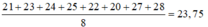




Đáp án D.
+ Trung bình cộng của dãy là x ¯ = 7
+ Phương sai của dãy số liệu thống kê là:
S 2 = 1 5 - 7 2 + 1 . 6 - 7 2 + 1 . 7 - 7 2 + 1 . 8 - 7 2 + 1 . 5 5 S 2 = 10 5 = 2